8.1. Опыты Фарадея. Работа по перемещению проводника с током в магнитном поле

Познакомимся с опытами, которые проводил Фарадей (рис. 8.3, 8.4).

 

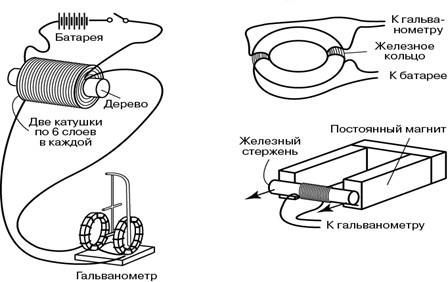
Рис. 8.3. Опыты Фарадея 

 

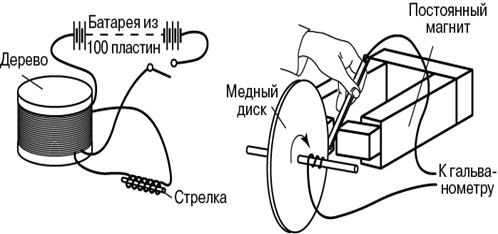
Рис. 8.4. Опыты Фарадея 

Для более близкого знакомства с явлением электромагнитной индукции, подробно рассмотрим два опыта (рис. 8.5).

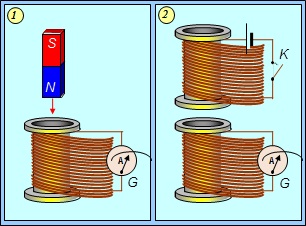
Рис. 8.5. ЭДС индукции возникает в катушке, когда:
1 — к нейприближается постоянный магнит; 2 — когда меняется ток в соседней катушке 

На левом рисунке изображена катушка, подсоединенная к гальванометру G. Если приближать к витку постоянный магнит, стрелка гальванометра отклонится: по катушке пройдет ток. При неподвижном же магните ничего не происходит. На правом рисунке вблизи такой же катушки с гальванометром помещена другая катушка. Если замкнуть ключ К, то по верхней катушке пойдет электрический ток. В этот момент стрелка гальванометра отклонится, зарегистрировав импульс тока в нижней катушке. То же самое произойдет при размыкании ключа К. 

Видео 8.2. Закон Фарадея: гибкий контур в магнитном поле катушек Гельмгольца.

В обоих случаях виток с гальванометром не был подсоединен к источнику тока. Тем не менее, ток в нем появился, что свидетельствует о возникновении какой-то электродвижущей силы. Ее называют ЭДС электромагнитной индукции. Рассмотренные опыты приводят к выводу, что ЭДС индукции возникает, когда что-то меняетсяв системе проводников. 

Обратимся к одному из возможных вариантов изменений в системе — перемещению одного из ее проводников. Поскольку на проводник с током действует сила, то при перемещении этого проводника будет совершаться работа. Рассмотрим устройство на рис. 8.6. 

 

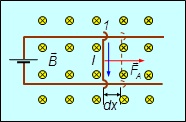
Рис. 8.6. Работа по перемещению проводника с током в магнитном поле 

Видео 8.3. К рисунку 8.6: возникновение индукционного тока при движении небольшого участка замкнутого проводящего контура в магнитном поле.

Пусть отрезок проводника с током  длиной перемещается из положения 1 в положение 2 под действием силы Ампера в магнитном поле

Работа, совершаемая полем по перемещению проводника на расстояние , равна

Произведение  есть элемент площади, которую пересек отрезок проводника при своем движении из положения 1 в положение 2. Таким образом,

где — изменение потока вектора магнитной индукции через площадь, охватываемую током.

Согласно (8.3) работа, совершаемая магнитным полем при перемещении в нем подвижного проводника с током, равна произведению силы тока I  в проводнике и потока  сквозь поверхность, заметаемую проводником при его движении. 

Полученному результату можно дать несколько иную интерпретацию. Токи, текущие в проводнике, так или иначе замкнуты, образуют контур. Если перемещать или деформировать контур с током во внешнем магнитном поле, то полная работа определится суммированием (интегрированием) элементарных работ

(8.4)

где и — значения потока магнитной индукции в начальном и конечном состоянии контура с током (мы предполагали, что ток в контуре при этом не меняется).

Пример 1. По кольцу радиусом 10 см, сделанному из тонкого гибкого провода, течет ток 100 А. Перпендикулярно плоскости кольца создано внешнее однородное магнитное поле 0,1 Тл. Направление этого поля совпадает с направлением собственного магнитного поля кругового тока на его оси. Определить работу А внешних сил, которую надо затратить, чтобы превратить кольцо в квадрат, не меняя его ориентации относительно внешнего поля. Работой против упругих сил пренебречь. Ток в кольце поддерживается постоянным. Как изменится результат, если внешнее поле будет иметь противоположное направление?

Решение. 1-й способ. Площадь кольца равна , так что поток магнитной индукции через кольцо равен . При деформации кольца в квадрат его периметр не изменится, так что сторона квадрата в четыре раза меньше длины окружности кольца

Его площадь равна

а магнитный поток

Поэтому величина работыбудет равна

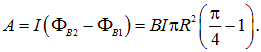
Подставляем численные значения и получаем

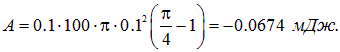
Работа получилась отрицательной, то есть ее надо совершить против сил поля. Действительно, при правовинтовом (по условию) расположении тока и внешнего поля сила Ампера стремится растянуть кольцо- увеличить его площадь. Превращая кольцо в квадрат, мы уменьшаем площадь, тем самым совершаем работу против сил поля.

Если поле имеет обратный знак, то эту работу совершит сила Ампера, и она будет положительной. При решении задачи в этом случаепотоквнешнего поля отрицателен (внешнее поле изменило своё направление на противоположное, а нормаль к поверхности, ограниченной контуром, осталась прежней, связанной правилом правого винта с направлением тока в контуре). Поэтому

и для работы  получится то же выражение, но с обратным знаком.

Решение. 2-й способ. Как известно, магнитный момент витка с током равен , а его потенциальная энергия в магнитном поле определяется выражением

При правовинтовом расположении тока и магнитного поля угол между векторами Р_m  и В  равен нулю, так что

Разность потенциальных энергий при деформации витка равна

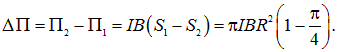
Поскольку , потенциальная энергия при деформации увеличилась, на что надо затратить работу против сил поля. При изменении направления поля угол между ним и магнитным моментом равен  , так что

и

Естественно, мы получили те же результаты, что и при первом способе решения.

Пример 2. Круглый виток с током 20 А свободно установился в однородном магнитном поле с магнитной индукцией 0,016 Тл. Радиус витка равен 5 см. Определить работу, которую надо совершить, чтобы повернуть виток на углы , ,  относительно оси, совпадающей с диаметром витка.

Решение. Раз в начальном положении виток установился свободно, значит его магнитный момент параллелен вектору В. Поток через плоскость витка положителен и равен . При повороте витка на угол  поток станет равным . Совершаемая при этом работабудет равна 

Отсюда находим

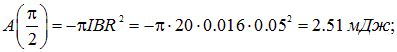
При углах поворота  работа отрицательна: контур находится в состоянии устойчивого равновесия, и надо затратить усилия против сил поля, чтобы вывести его из равновесного состояния. Но при  контур уже сам стремится к положению равновесия, так что работа будет совершаться силами поля, и это частично компенсирует затраченную прежде работу. При полном обороте работа сил поля в точности равна работе внешних сил, так что полная работа оказывается равной нулю.

Этот пример также можно решить другим способом — в терминах потенциальной энергии взаимодействия магнитного момента с полем.

Отметим, что использовать для вычисления работы магнитный момент контура с током можно лишь в том случае, если внешнее поле однородно или слабо неоднородно. Последнее означает, что внешнее поле в пределах контура меняется настолько мало, что этим можно пренебречь. Если внешнее поле в пределах контура меняется существенно, то точный результат для работы может быть получен только путем интегрирования работы сила Ампера с учетом величины и направления внешнего поля в точке её приложения. Такой подход и приводит к точной формуле (8.4), полученной выше на примере системы простейшей геометрии, изображенной нa рис. 8.2. Таким образом, формула (8.4) точная и общая — для задачи любой геометрии.

 

Дополнительная информация

http://rack1.ul.cs.cmu.edu/is/faraday/  — опыты Фарадея;

http://www.juliantrubin.com/bigten/faradaycageexperiments.html — изобретения и открытия Фарадея.