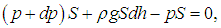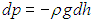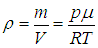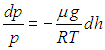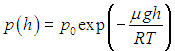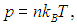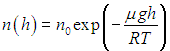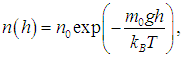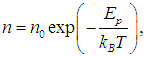3.4. Распределение молекул по координатам

В этом разделе мы перейдем теперь к анализу распределения молекул газа по координатам. Очевидно, что если на молекулы газа не действуют внешние силы, то, в состоянии термодинамического равновесия, газ равномерно распределен по заданному объему. В этом случае давление и плотность газа одинаковы во всех точках. Если же газ находится в силовом поле (как, например, атмосферный воздух, который испытывает притяжение Земли), то давление и плотность газа уже не будут всюду одинаковыми, а будут меняться от точки к точке.

Видео 3.4. Распределение молекул газа по высоте сосуда, находящегося в однородном поле тяжести.

Барометрическая формула. Найдем закон, по которому изменяется давление атмосферы (или плотность воздуха) по мере удаления от поверхности Земли. Выделим вертикальный столб воздуха с площадью горизонтального сечения S.

Предположим, что

• этот столб находится в тепловом равновесии, то есть температура везде одинакова (в реальной атмосфере это не так, но для простоты анализа будем предполагать Т = const);
• газ идеальный, то есть для него справедливо уравнение Клапейрона — Менделеева

 

• можно пренебречь изменением ускорения свободного падения g с высотой (что справедливо для не очень больших высот).

Атмосферное давление на высоте h обусловлено весом вышележащих слоев газа. Пусть на высоте h давление р, тогда на высоте h + dh давление р + dp (рис. 3.6). При этом, если dh > 0, то давление уменьшается, dp < 0, так как уменьшается вес вышележащих слоев атмосферы.

Рис. 3.6. Вертикальный воздушный цилиндр (к выводу барометрической формулы)

Выделенный слой газа, высотой dh и массой m, находится в равновесии. Следовательно, сумма действующих на него сил равна нулю:

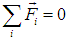
В проекции на вертикальную ось получаем

где r — плотность газа на высоте h. Раскрывая скобки и приводя подобные члены, переходим к уравнению

Воспользуемся уравнением Клапейрона — Менделеева для выделенной массы газа m и выразим плотность через давление:

Подставляя (3.47) в (3.46), окончательно получаем

Это уравнение можно проинтегрировать в случае изотермической атмосферы (Т = const):

Видео 3.5. Барометрическая формула: язычок пламени в роли весьма чувствительного индикатора убывания давления с высотой.

Постоянная интегрирования р₀ равна давлению на поверхности (h = 0). Полученная зависимость называется барометрической формулой. Она описывает распределение давления газа по высоте в однородном поле тяжести при постоянной температуре. Следует обратить внимание на то, что распределение зависит от рода газа. Чем меньше m, тем меньше по абсолютной величине показатель степени, и тем медленнее для такого газа уменьшается давление при увеличении высоты. На рис. 3.7 показаны зависимости давления от высоты при температуре Т = 300 К (27 °С) для трех газов различной молярной массы — водорода Н₂ (m₁ = 2,016 г/моль), азота N₂ (m₂ = 28,013 г/моль) и кислорода 0₂ (m₃ = 31,999 г/моль).

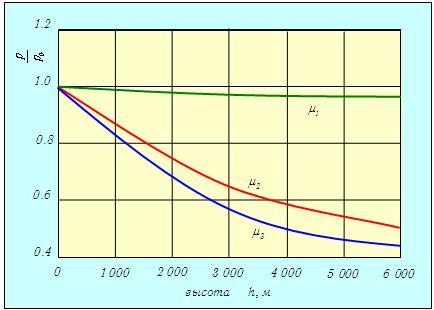
Рис. 3.7. Зависимость давления трех разных газов Н₂, N₂ и O₂ от высоты

Пример. Определим, на какой высоте давление кислорода уменьшается в два раза (при Т = 300 К).

Применяем барометрическую формулу.

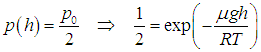
Тогда

откуда

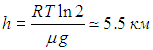
Используя уравнение идеального газа в форме

из барометрической формулы легко получить закон изменения с высотой числа n молекул в единице объема:

Из (3.51) следует, что состав воздуха с ростом высоты будет меняться количественно: возрастет концентрация газов с малой молярной массой, например водорода и гелия.

У поверхности воздух представляет собой смесь газов: N₂ — 78,08 %, O₂ — 20,95 %, СO₂ — 0,03 %, инертные газы — 0,94 %. Посмотрим, как изменится отношение концентраций кислорода и азота в изотермической атмосфере (Т = 300 К) на высоте 10 км.

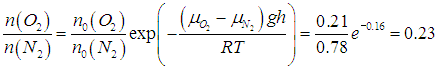
Отношение концентраций кислорода и азота уменьшится от 0,27 до 0,23. Наш расчет справедлив лишь для изотермической атмосферы и сравнительно небольших высот, для которых ускорение свободного падения изменяется незначительно: g = const, T = const.

Распределение Больцмана. Число молекул в единице объема зависит от высоты h и температуры Т, причем обе переменные входят в показатель экспоненты. Уравнение (3.51) можно записать в виде

где k_B — масса одной молекулы газа. При этом выражение m₀gh, стоящее в числителе, есть не что иное, как потенциальная энергия одной молекулы в поле тяжести Земли. Поэтому можно говорить, что мы имеем распределение молекул по значениям потенциальной энергии. При этом чем больше потенциальная энергия, тем меньше таких молекул. В знаменателе показателя степени стоит k_BТ — величина, пропорциональная средней энергии теплового движения молекулы. Чем выше температура, то есть чем больше энергия теплового движения молекул, тем экспоненциальный множитель, пропорциональный концентрации молекул, с ростом высоты убывает медленнее. На рис. 3.8 показаны кривые относительной концентрации молекул кислорода O₂ на разных высотах при двух различных температурах Т₁ = 300 К и Т₂ = 1 300 К (последний случай, конечно, нереален и используется лишь как иллюстрация).

Рис. 3.8. Зависимость относительной концентрации молекул кислорода от высоты при разных температурах T₁ = 300 K и T₂ = 1 300 K

Видно, что число частиц в единице объема при большей температуре медленнее убывает с высотой. При уменьшении температуры большая часть частиц располагается на меньшей высоте. А при Т = 0 все частицы расположились бы на поверхности Земли. Этот факт имеет простое физическое объяснение. Каждое конкретное распределение молекул по высоте устанавливается в результате действия двух тенденций:

• притяжение молекул к Земле, характеризуемое потенциальной энергией m₀gh, стремится расположить их на поверхности Земли;
• тепловое движение, характеризуемое энергией k_BТ, стремится разбросать молекулы по всем высотам равномерно.

Обозначив Е_р = m₀gh, получим

то есть концентрация молекул больше там, где меньше их потенциальная энергия. Частицы будут с большей вероятностью располагаться в тех точках пространства, где потенциальная энергия меньше.

Больцман доказал, что такое распределение осуществляется в поле любых сил, а не только в гравитационном поле. Поэтому распределение (3.53), где n — концентрация частиц с потенциальной энергией Е_р называется распределением Больцмана.