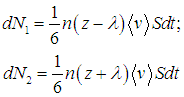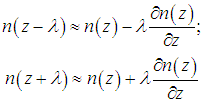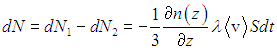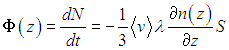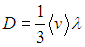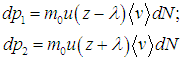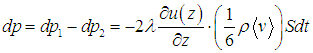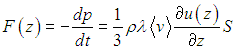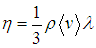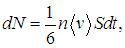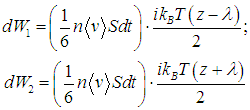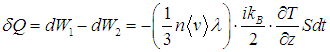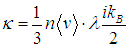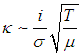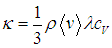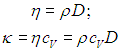4.3. Кинетическая теория переноса
Изложенные выше законы, описывающие явления переноса — первый закон Фика и аналогичные законы для внутреннего трения и теплопроводности, — были установлены экспериментально. В этом разделе мы покажем, что они следуют из молекулярно-кинетической теории. Основу всех явлений переноса составляет хаотическое движение молекул. При переходе в другие части системы молекулы переносят туда информацию о тех условиях, в которых они пребывали прежде. Перенос массы (или сам переход частиц) характерен для явления диффузии. Перенос энергии от одних слоев газа к другим составляет сущность процесса теплопроводности. И, как мы увидим, перенос импульса лежит в основе явления внутреннего (молекулярного) трения газа или жидкости.
Диффузия. Проведем сначала анализ процесса диффузии (точнее, самодиффузии, то есть диффузии каким-то образом выделенных молекул в среде, состоящей из таких же частиц). В этом случае средние скорости частиц среды и диффундирующих частиц одинаковы, а длина свободного пробега дается уже знакомым выражением
![]()
Выделим мысленно в среде какую-то площадку S и направим ось z ортогонально к ней. Две другие оси х и у параллельны площадке. Хаотичность движения молекул смоделируем следующим образом. Будем считать, что ровно 1/3 молекул движется вдоль оси х, 1/3 — вдоль оси у и 1/3 — вдоль оси z. Из молекул, летящих параллельно z, ровно половина (1/6 часть полного числа молекул) движется в положительном направлении, и столько же - в отрицательном. Подсчитаем количество молекул, пересекающих площадь S в единицу времени (рис. 4.8).
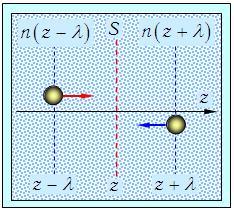
Рис. 4.8. Встречные потоки частиц через площадку S из областей с различной концентрацией частиц (к выводу первого закона Фика)
Ясно, что молекулы, летящие вдоль осей х и у, площадку не пересекут. За время dt молекулы преодолевают расстояние <v>dt. Потому на площадку попадет только 1/6 часть молекул из объема <v>dtS справа и 1/6 часть молекул из того же объема слева. Но концентрации частиц слева и справа различны (n зависит от z).
Внимательный читатель может спросить: ведь мы фиксируем бесконечно малый промежуток времени dt, следовательно, и рассматриваемые объемы — диски бесконечно малой толщины <v>dt. Поэтому, казалось бы, и концентрации частиц слева и справа должны совпадать. Вопрос правилен, но дело в том, что последний раз перед попаданием на площадку S молекулы сталкивались с другими молекулами на расстоянии длины свободного пробега l от площадки. Поэтому к выделенной нами площади они подходят с теми концентрациями частиц n(z – l) и n(z + l), которые сложились в точках с координатами z – l и z + l соответственно (z — координата площадки). Слева на площадку попадет число частиц dN1, a справа — dN2, причем эти числа будут различаться:
|
|
|
(4.16) |
Поскольку l мало, можем разложить концентрации частиц в ряд, удерживая только два первых члена:
|
|
|
(4.17) |
Полное число частиц dN, пересекающих площадку в положительном направлении оси z, равно разности чисел частиц, пересекающих площадку слева и справа. Находим тогда
|
|
|
(4.18) |
Выражение для потока частиц
|
|
|
(4.19) |
по структуре в точности совпадает с первым законом Фика (4.7). Стало быть, мы не только вывели этот закон, но и определили коэффициент диффузии:
|
|
|
(4.20) |
Учитывая, что
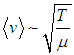
и что
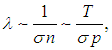
|
|
|
(4.21) |
Такая зависимость коэффициента диффузии в газах от температуры и давления подтверждается экспериментом.
Вязкость. Рассмотрим теперь механизм возникновения вязкости газа. Ось z теперь будем представлять расположенной вертикально в соответствии с рис. 4.9.
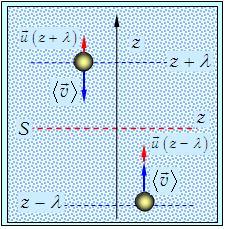
Рис. 4.9. Встречные потоки частиц через площадку S из областей с различной скоростью упорядоченного движения частиц (к выводу закона вязкости)
Предположим теперь, что концентрация частиц одинакова во всех частях системы, так что числа частиц
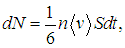
приходящих снизу и сверху, равны. Однако молекулы приходят из слоев, имеющих разные скорости упорядоченного (не молекулярного!) движения u(z). Когда более медленная молекула из нижнего слоя попадает в верхний, она притормаживает его упорядоченное движение, а сама ускоряется. Наоборот, молекулы из верхнего слоя ускоряют нижний и тормозятся им. Таким образом, этот процесс способствует выравниванию скоростей в системе, а именно в этом и заключается явление внутреннего трения (вязкости).
Мы предполагаем, что скорость упорядоченного движения много меньше средней скорости теплового движения молекул (составляющей сотни метров в секунду). Тогда среднюю скорость теплового движения <v> можно по-прежнему считать постоянной. Для импульсов упорядоченного движения, переносимого через площадь S снизу и сверху, имеем
|
|
|
(4.22) |
Отсюда для полного импульса, переносимого в положительном направлении оси z, получаем
|
|
|
(4.23) |
В этой формуле мы использовали плотность газа
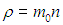
Переносимый импульс параллелен скорости u, а его направление зависит от знака производной. При распределении скоростей, показанном на рис. 4.3, скорость растет с ростом z, так что производная
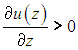
Знак минус в уравнении (4.23) означает, что импульс, поступающий снизу от более медленных слоев, меньше импульса, поступающего сверху, от более быстрых слоев. Поэтому импульс слоя с координатой z в данном случае стремится возрасти на величину –dp. Производная
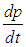
дает силу, действующую на слой жидкости площадью S и имеющий координату z
|
|
|
(4.24) |
Мы вывели закон (4.14) и получили выражение для коэффициента динамической вязкости
|
|
|
(4.25) |
Теперь нетрудно установить зависимость коэффициента динамической вязкости от температуры и рода газа:
|
|
|
(4.26) |
Обратите внимание, что коэффициент динамической вязкости не зависит в конечном итоге от плотности, то есть от давления. Это происходит потому, что с ростом давления увеличивается плотность газа, но и пропорционально растет концентрация частиц, то есть уменьшается длина свободного пробега. Эти два фактора компенсируют друг друга.
Теплопроводность. Проанализируем теперь явление теплопроводности. Предположим, что концентрация частиц в системе всюду одинакова, так что слева и справа площадку пересекает одинаковое число частиц, как и при рассмотрении диффузии:
|
|
|
(4.27) |
так что полный поток частиц через площадку S (рис. 4.10, сравни с рис. 4.8) равен нулю.
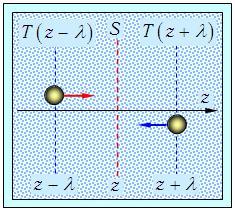
Рис. 4.10. Встречные потоки частиц через площадку S из областей с различной температурой газа (к выводу закона теплопроводности)
Однако молекулы приносят с собой те средние энергии w, которыми они обладали в слоях с координатами z – l и z + l. Эти энергии пропорциональны температуре:
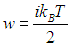
Умножая среднюю энергию на число частиц, пересекающих площадку, получаем для переносимого ими количества энергии слева и справа
|
|
|
(4.28) |
Для тепла, переносимого в положительном направлении оси z, отсюда получаем выражение
|
|
|
(4.29) |
Мы вывели закон (4.15) и нашли коэффициент теплопроводности
|
|
|
(4.30) |
Видео 4.3. Теплопроводность газов. Бутан – воздух при одинаковых и разных давлениях.
Напомним, что i — эффективное число определяющее среднюю энергию молекулы. Поскольку
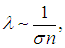
то коэффициент теплопроводности не зависит от концентрации молекул или плотности газа. Зависимость его от температуры Т и рода газа такова:
|
|
|
(4.31) |
Видео 4.4. Теплопроводность газов. Неон – воздух при одинаковом давлении.
Видео 4.5. Теплопроводность газов. Воздух – воздух при разном давлении.
Введем удельную теплоемкость газа при постоянном объеме
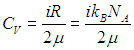
и учтем далее, что масса молекулы равна
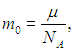
откуда следует связь концентрации частиц с плотностью газа
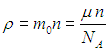
Тогда получим для коэффициента теплопроводности несколько иное выражение:
|
|
|
(4.32) |
Из проведенного анализа следуют формулы связи между соответствующими коэффициентами переноса (см. соотношения (4.20), (4.25) и (4.32)):
|
|
|
(4.33) |
Приведем численные оценки, использовав полученные ранее результаты для водяного пара, характерные при нормальных условиях для всех газов: плотность
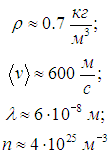
Тогда находим коэффициенты диффузии
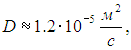
теплопроводности (i = 6 для водяного пара)
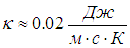
и динамической вязкости
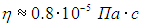
Сравним полученные оценки с опытными данными для воздуха:
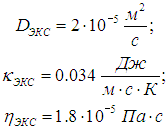
Мы видим, что не ошиблись, по крайней мере, в порядках величин, хотя наши оценки коэффициентов и не совсем точны.
Дополнительная информация
http://www.plib.ru/library/book/14222.html — Яворский Б.М., Детлаф А.А. Справочник по физике, Наука, 1977 г. — стр. 214 — сводная таблица явлений переноса в газах.