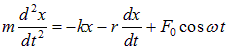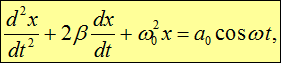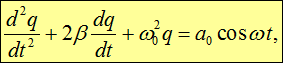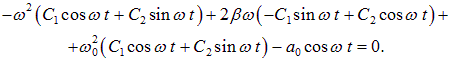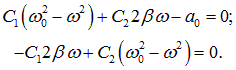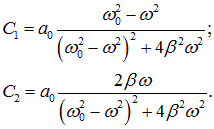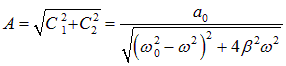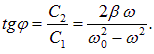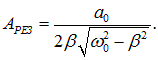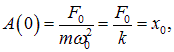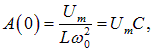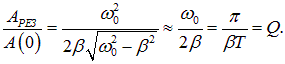1.7. Вынужденные колебания

В случае вынужденных колебаний система колеблется под действием периодической внешней (вынуждающей) силы. За счет работы этой силы компенсируются потери энергии системы. Частота вынужденных колебаний зависит от частоты изменения внешней силы (для краткости мы будем называть её "вынуждающей частотой"). Практически наиболее интересным является случай, когда вынуждающая сила изменяется по гармоническому закону:

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом.

Видео 1.21 Резонансное взаимодействие маятников

Видео 1.22 Камертоны: резонансное поглощение энергии волны

Видео 1.23 Резонанс доски с мотором

Явление резонанса используется для усиления колебаний, например электрических. Однако при конструировании машин и сооружений необходимо учитывать явление резонанса, чтобы предотвратить чаще всего нежелательные, а иногда и разрушительные последствия резонансного увеличения амплитуды вынужденных колебаний.

Для пружинного маятника уравнение вынужденного колебательного движения имеет вид:

или

где

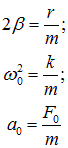
и    — вынуждающая частота.

Если рассматривать электрический колебательный контур, то компенсировать потери энергии в контуре можно с помощью подводимой извне периодически изменяющейся по гармоническому закону ЭДС или переменного напряжения

 

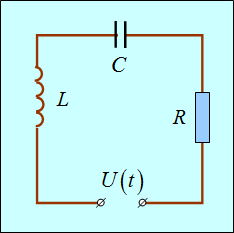
Рис. 1.25. Вынужденные колебания в электромагнитном контуре

Уравнение колебаний в контуре (рис. 1.25) можно записать, используя закон Ома для замкнутой цепи

или, с учетом, что

 

где

— собственная частота контура,

— коэффициент затухания, a

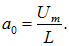
Таким образом, вынужденные колебания в электрическом контуре описываются тем же самым линейным неоднородным дифференциальным уравнением второго порядка, что и в случае колебаний пружинного маятника. Предположим, что нам известно хотя бы одно решение этого уравнения — некое частное решение . Тогда разность любого другого решения q(t) и этого частного решения  будет удовлетворять однородному уравнению (с нулем в правой части), которое мы подробно изучили в предыдущем разделе. Поэтому общее решение уравнения (1.87) может быть записано как

где

— частота свободных затухающих колебаний.

С течением времени из-за экспоненциального множителя  роль второго слагаемого уменьшается (оно важно на начальной стадии установления колебаний). По прошествии достаточно большого времени, а именно, при

,

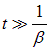им можно пренебречь, сохраняя лишь первое слагаемое. Таким образом, задача исследования установившихся вынужденных колебаний сводится к нахождению хотя бы одного частного решения уравнения (1.87).

Частное решение неоднородного уравнения будем искать в виде гармонической функции, частота изменения которой совпадает с частотой вынуждающей силы:

Подставим  в виде (1.89) в уравнение (1.87):

Так как функции синуса и косинуса линейно независимы, коэффициенты при них в левой части (1.90) должны быть равны нулю:

Решение этой системы имеет вид:

Решение (1.89) с коэффициентами (1.92) можно записать в стандартном виде:

где

и

При знаке минус в фазе косинуса в выражении (1.93) начальная фаза  имеет простой физический смысл: это отставание по фазе установившегося вынужденного колебания от гармонической вынуждающей «силы» (1.85).

Видео 1.24 Резонансный язычковый частотомер

Видео 1.25 Спектр модулированного колебания

Рассмотрим отклик системы на изменение частоты внешней силы. Под квадратным корнем в выражении для амплитуды стоит квадратичная функция частоты

Эта функция имеет минимум (а значит, амплитуда имеет максимум).

Для нахождения точки минимума дифференцируем функцию  по  и приравниваем производную нулю. В итоге получаем следующие выражения для резонансной частоты

и амплитуды установившихся вынужденных колебаний при резонансе

Следует отметить, что при  значение резонансной частоты   практически совпадает с собственной частотой  колебательной системы. Поскольку   стоит в знаменателе выражения для , резонансная амплитуда колебаний растет с уменьшением затухания. На графике 1.26 видно, что чем меньше затухание, тем выше и правее лежит максимум резонансной кривой.

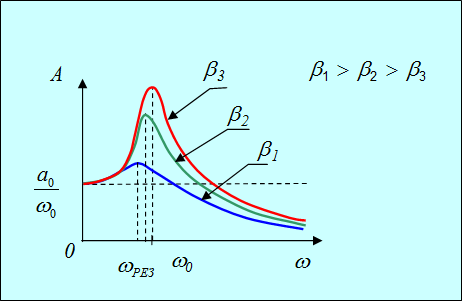
Рис. 1.26. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы

При увеличении частоты внешнего воздействия амплитуда стремится к нулю:

Физически это понятно: система обладает некой инерционностью и не успевает следовать за быстрыми изменениями внешнего воздействия. В другом предельном случае малой внешней частоты

мы имеем дело со статическим случаем — действием постоянной внешней силы F₀ на пружинный маятник, или подсоединением контура к источнику с постоянным напряжением U_m. В этом случае предельное значение амплитуды вынужденных колебаний равно

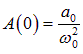
и не зависит от затухания. Последнее вполне естественно, так как затухание обусловлено действием силы сопротивления, которая пропорциональна скорости и проявляется только при движении системы, а не в статическом пределе. В случае механических колебаний

что равно удлинению пружины под действием постоянной силы F₀.

В случае электромагнитных колебаний в контуре

что равно заряду на конденсаторе при подсоединении его к источнику постоянного напряжения U_m.

Найдем отношение резонансной амплитуды к статической при малом затухании, когда :

Иными словами, добротность Q характеризует также резонансные свойства колебательной системы: чем больше добротность, тем выше и относительно уже резонансный пик (см. рис. 1.26).

Автоколебательные системы. Параметрический резонанс.

Видео 1.26 Анкерный механизм механических часов

Видео 1.27 Колебания линейки под струёй воды

Видео 1.28 Спираль Роже

Видео 1.29 Параметрический резонанс

 

Дополнительная информация

http://class-fizika.spb.ru/index.php/slaid/193-kol – Много интересных анимаций, видео, слайд-шоу по колебаниям и волнам.

http://www.fxyz.ru/формулы_по_физике/колебания_и_волны – Основные формулы по колебаниям и волнам (см. Также раздел «подтемы» справа вверху)

http://physics-lectures.ru/category/mexanicheski-kolebaniya-i-volny/ – Лекции по колебаниям и волнам

http://www.alleng.ru/d/phys/phys105.htm – Д.В. Сивухин. Электричество, колебания и волны. Учебник.

http://www.ph4s.ru/book_ph_koleb.html  – Ссылки на книги по колебаниям и волнам. Сайт бывшего преподавателя МИФИ А.Н. Варгина.

http://fmclass.ru/math.php?id=485a8e5cc78f8 – Статьи по колебаниям и оптике из журнала «Квант»

http://www.physel.ru/mainmenu-48.html – Полезные материалы по колебаниям и волнам.

http://koi.tspu.ru/waves/index.htm – А.Г.  Парфенов, Электронный мультимедиа-учебник по колебаниям и волнам

http://www.alleng.ru/d/phys/phys126.htm – Савельев, Курс общей физики. Т.1 – Механика, колебания и волны, молекулярная физика.

http://www.alleng.ru/d/phys/phys260.htm – А.Я. Исаков , В.В. Исакова.  Колебательные и волновые процессы, руководство по самостоятельной работе.

http://lib.mexmat.ru/books/6452 – Г.С. Ландсберг.  Элементарный учебник физики. Колебания и волны. Оптика. Атомная и ядерная физика.

http://elkniga.ucoz.ru/ – Г.Я. Мякишев, А.З. Синяков. Учебник по колебаниям и волнам для углубленного изучения в 11-м классе.

http://repetitor.mathematic.of.by/spravka_fizika.htm#M2 – Основные формулы по механике, в том числе – по колебаниям.

 http://www.alleng.ru/d/phys/phys194.htm – Л.Н. Коршунова. Колебания и волны. Пособия по решению задач.

 http://fizportal.ru/fluctuation-b – Банк задач по колебаниям и волнам с решениями.

http://www.alleng.ru/d/phys/phys127.htm – Савельев, Курс общей физики. Т.2 — Электричество и магнетизм. Волны. Оптика.

http://ligis.ru/effects/science/238/index.htm – Эффект механического резонанса.

http://schools.keldysh.ru/sch1216/students/spr_resh_zad/wob_wave/wob_wave1.htm – Задачи по колебаниям и волнам с решениями.

http://sgtnd.narod.ru/papers/TASKS.pdf – А.П. Кузнецов, А.Г. Рожнев, Д.И. Трубецков. Линейные колебания и волны. Сборник задач.

http://www.phys.kemsu.ru/viewpage.php?page_id=178 – Задачи по колебаниям и волнам повышенной сложности для старшеклассников.

http://physbook.ru/index.php/PPT._Маятник_Фуко – Маятник Фуко. История, модели.