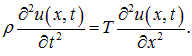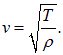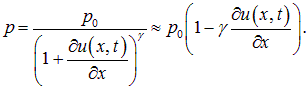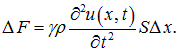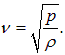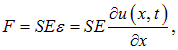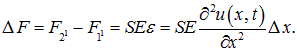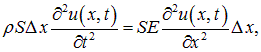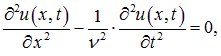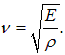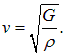2.1. Волны в упругих средах

Колебания струны 

Рассмотрим малые колебания струны, натянутой силой Т вдоль оси х. Пусть смещение произвольной точки струны с координатой х в момент времени t есть вектор . Ограничимся простейшим колебательным процессом, когда все векторы смещения  в любой момент времени перпендикулярны оси х и лежат в фиксированной плоскости. Тогда смещения точек струны можно описать одной скалярной функцией , как показано на рис. 2.1.

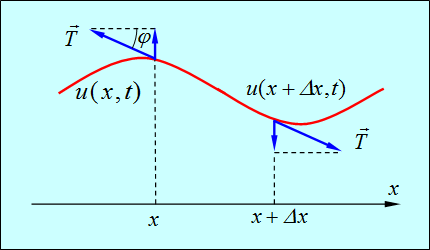
Рис. 2.1. Колебания струны

Напряжения, возникающие в струне, направлены по касательным к ее мгновенному профилю. Мы будем рассматривать малые колебания, когда можно пренебречь удлинением струны и возникающими при этом дополнительными силами упругости. Тогда натяжение струны можно считать постоянным для всех моментов времени t и точек х. Выделим элемент струны, лежащий между координатами х и  . Рассмотрим точку с координатой х. Тангенс угла наклона силы T, действующей на этот край элемента, равен

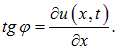
Вертикальная компонента силы равна

Так как угол  мал, то

Тогда

Аналогично, вертикальная компонента силы натяжения струны, действующей на другом конце выделенного элемента, равна

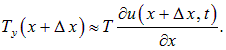
Равнодействующая этих сил равна

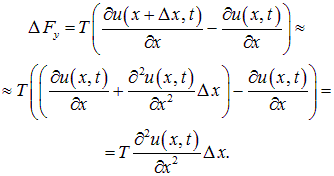
Заметим, что горизонтальные компоненты силы натяжения

не зависят от положения точки и потому их равнодействующая равна нулю. Это означает, что в рассматриваемом приближении элементы струны движутся только в вертикальном направлении.

Если линейная плотность (масса единицы длины) струны равна , то масса элемента равна

Записываем уравнение второго закона Ньютона для вертикального смещения элемента струны:

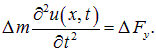
Подставляя сюда выражение для , получаем уравнение движения струны:

Это уравнение можно переписать в виде:

где

Определим размерность величины . Размерность силы

размерность линейной плотности материала струны

Отсюда размерность величины будет

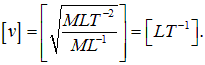
то есть величина имеет размерность скорости.

Колебания в идеальном газе

Рассмотрим колебания в газе, происходящие вдоль одной оси х. В отличие от струны частицы газа смещаются здесь в продольном направлении, но величины смещения мы будем обозначать тем же символом u(x,t).

Рассмотрим элементарный объем газа V₀, ограниченный сечениями 1 и 2, находящимися в точке с координатами х и  (рис. 2.2). Масса газа в объеме равна , где   — плотность газа, a S — площадь поперечного сечения. В равновесном стационарном состоянии давление газа равно .

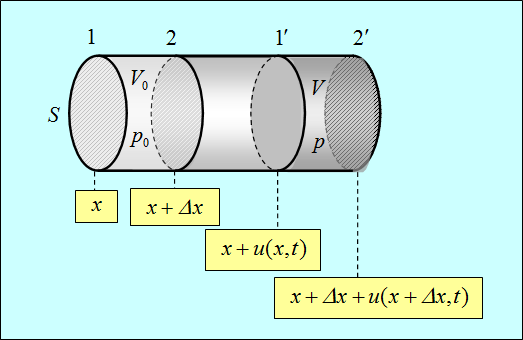
Рис. 2.2. Колебания в газе

При колебаниях выделенный объем смещается в новое положение между сечениями 1' и 2' с координатами

и

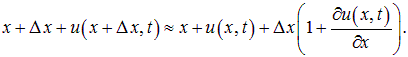
Объем газа в новом положении становится равным

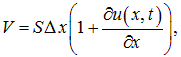
а давление в нем — р. Найдем это давление.

Колебательные процессы в газах происходят достаточно быстро, так что можно считать, что элементарный объем не успевает обмениваться теплотой с соседними объемами. Значит, процесс можно считать адиабатным. Записываем уравнение этого процесса:

или

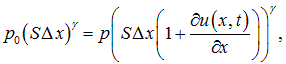
откуда

Здесь  — показатель адиабаты, зависящий от вида газа. Мы использовали также малость производной

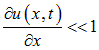
для разложения в ряд:

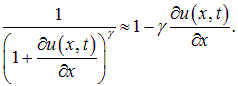
Составим теперь уравнение движения элементарного объема. Его ускорение равно

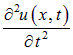
Сила, действующая на объем, определяется разностью давлений в сечениях 1' и 2':

Подставляя сюда выражение для давления р находим:

Записываем теперь уравнение второго закона Ньютона

или

После очевидных сокращений это уравнение можно представить в виде:

где

Величина имеет размерность скорости. Уравнение колебаний газа совпало с уравнением колебаний струны (2.2), хотя они описывают процессы в совершенно различных физических системах.

Колебания в твердых телах

Колебательные процессы в твердых телах похожи на колебания в газах. На рис. 2.3 представлена продольная деформация твердого тела в направлении оси х.

Рис. 2.3. Продольные колебания в твердом теле

Относительная деформация элементарного объема при смещении u равна

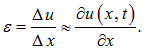
Согласно закону Гука, это приводит к появлению упругой силы

где Е — коэффициент (модуль Юнга), характеризующий жесткость среды. Равнодействующая сил упругости, действующих в сечениях 1' и 2' равна:

Записывая второй закон Ньютона в виде:

находим уравнение колебаний в твердом теле:

где

Размерность модуля Юнга совпадает с размерностью давления, так что  и здесь имеет размерность скорости.

Видео 2.1 Механическая модель 1 продольной волны

Выше мы рассматривали продольные смещения в твердом теле. В отличие от газов, упругие силы возникают в твердых телах и при деформации сдвига. Уравнение для таких поперечных колебаний имеет тот же вид (2.13), но вместо модуля Юнга в выражении для v будет стоять так называемый модуль сдвига G:

Видео 2.2 Механическая модель 2 продольной волны и поперечной волн

Механизм распространения продольных и поперечных колебаний показан на рис. 2.4 и 2.5.

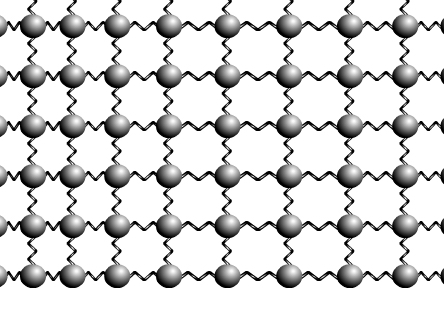
Рис. 2.4. Продольные волны в твердом теле

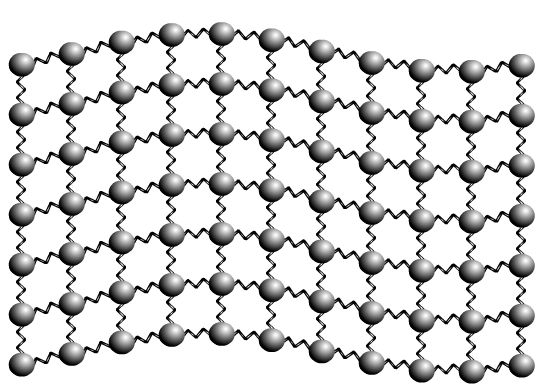
 Рис. 2.5. Поперечные волны в твердом теле

 

Дополнительная информация

http://files.school-collection.edu.ru/dlrstore/b7ad9b74-6ecd-42bb-98c8-00d96af3da5e/151.avi – Что такое поперечные волны. Анимация.

http://files.school-collection.edu.ru/dlrstore/a57a06f5-66cb-4403-8416-ad9b2b2cbe80/9_23.avi – Продольные волны, пример из детства. Видео.