5.1. Принцип Гюйгенса — Френеля

Изложенный ранее принцип Гюйгенса имеет характер геометрического правила. Согласно принципу Гюйгенса, каждую точку волнового фронта можно рассматривать как самостоятельный источник колебаний, а результат действия вторичных волн может быть найден построением поверхности, огибающей эти вторичные волны. Французский физик О. Френель дополнил этот принцип, предложив рассматривать волновое возмущение в любой точке пространства как результат интерференции вторичных волн от фиктивных источников, расположенных на волновом фронте. Эти фиктивные источники когерентны, и поэтому могут создавать интерференционную картину в любой точке пространства, в результате чего элементарные волны могут гасить или усиливать друг друга.

Способ Френеля вкладывает более глубокое физическое содержание в принцип Гюйгенса, а также позволяет решить ряд задач, представлявших трудности в рамках первоначального принципа Гюйгенса.

Рассмотрим поверхность волнового фронта S (рис. 5.1).

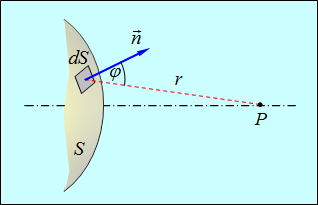
Рис. 5.1. Применение принципа Гюйгенса — Френеля к сферической волне

В соответствии с принципом Гюйгенса — Френеля

Для сферической волны амплитуда убывает с расстоянием r от источника как 1/r. Следовательно, от каждого элемента dS волновой поверхности в точку наблюдения Р приходит колебание

где  — амплитуда светового колебания в точке волновой поверхности, где расположен элемент dS, пропорциональная его площади;  — коэффициент, который уменьшается с ростом угла  между нормалью n к площадке dS и направлением от dS к точке наблюдения Р. Результирующее колебание в точке Р представляет суперпозицию элементарных колебаний dE, причем интеграл берется по всей волновой поверхности S:

Это соотношение представляет аналитическое выражение принципа Гюйгенса — Френеля.

В общем случае расчет интерференции вторичных волн довольно сложен и громоздок, однако для ряда задач нахождение амплитуды результирующего колебания оказывается возможным с помощью алгебраического или геометрического суммирования.