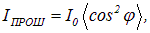6.1. Поляризация света

Следствием теории Максвелла является поперечность электромагнитных (световых) волн распространяющихся в вакууме или изотропной среде: векторы напряженности электрического и магнитного полей волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости v распространения волны (то есть перпендикулярно световому лучу). Явление поляризации света служит надежным обоснованием поперечности световой волны. При рассмотрении поляризации обычно все рассуждения связывают с плоскостью колебаний вектора напряженности электрического поля Е — светового вектора, так как химическое, физиологическое и другие виды воздействия света на вещество обусловлены главным образом электрическими колебаниями. Однако при этом следует помнить об обязательном существовании перпендикулярного ему вектора напряженности магнитного поля Н.

Поляризация электромагнитной волны. Записывая решение для электрического поля плоской электромагнитной волны в виде

мы предполагали, что направление вектора амплитуды колебаний  не зависит от времени. В этом случае вектор электрического поля всегда и во всех точках волны направлен вдоль одной и той же прямой — колеблется в одной плоскости неизменной ориентации в пространстве.

Выбирая ось х вдоль направления распространения волны, а ось у —  вдоль векторной амплитуды , записываем (6.1) в виде

Однако существует и вторая линейно поляризованная волна, имеющая ту же частоту и распространяющаяся в том же направлении:

Электрические колебания в этой волне направлены вдоль оси z, так что волны (6.2) и (6.3) линейно независимы. Обе они являются решением одного и того же волнового уравнения, так что их суперпозиция также является решением того же уравнения. Сложив эти волны, мы найдем общее выражение для монохроматической волны с данной частотой w, распространяющейся вдоль оси х. Математически эта процедура ничем не отличается от сложения взаимно ортогональных колебаний. Если зафиксировать какую-то точку х и следить за изменением вектора электрического поля в ней, то конец вектора  будет описывать эллиптическую, в общем случае, траекторию в плоскости, параллельной y0z. Вращение вектора  происходит с частотой волны . В этом случае говорят, что свет имеет эллиптическую поляризацию. Если разность фаз  кратна , то эллиптическая поляризация вырождается в линейную. При равенстве амплитуд Е_0,у и Е_0,г эллипс превращается в окружность. Тогда говорят о круговой поляризации волны. В соответствии с двумя возможными направлениями вращения вектора  возможны право- и левополяризованные волны. Любую электромагнитную волну можно представить как линейную комбинацию двух линейно поляризованных волн или как линейную комбинацию двух волн с круговой поляризацией. Иными словами, электромагнитные волны имеют две внутренние степени свободы.

Естественный и поляризованный свет. В свете, испускаемом обычными источниками, имеются колебания, совершающиеся в различных направлениях, перпендикулярных к лучу. В таких световых волнах, исходящих из различных элементарных излучателей (атомов), векторы  имеют различные ориентации, причем все эти ориентации равновероятны, что обусловлено большим числом атомных излучателей. Такой свет называется естественным, или неполяризованным.

Если под влиянием внешних воздействий на свет или внутренних особенностей источника света (лазер) появляется предпочтительное, наиболее вероятное направление колебаний, то такой свет называется частично поляризованным. Неполяризованный (естественный) свет может испускаться лишь огромным числом элементарных излучателей. Электромагнитная волна от отдельного элементарного излучателя (атома, молекулы) всегда поляризована. С помощью различных поляризаторов из пучка естественного света можно выделить часть, в которой колебания вектора  будут происходить в одном определенном направлении в плоскости, перпендикулярной лучу, то есть выделенный свет будет линейно поляризованным.

На рисунках направление колебаний электрического поля линейно поляризованной волны изображается следующим образом. Если вектор Е колеблется в плоскости чертежа, то на направление вектора скорости волны  наносится ряд вертикальных стрелочек (рис. 6.1-1), а если в плоскости, перпендикулярной чертежу, — ряд точек (рис. 6.1-2). Естественный (неполяризованный) свет условно обозначается чередующимися черточками, которым соответствует, например, компонента Е_y вектора напряженности электрического поля, и точками, соответствующими другой компоненте Е_z (рис. 6.1-3).

Рис. 6.1. Условные обозначения типа  поляризации волны 

Существуют приборы (поляризаторы), пропускающие только колебания, происходящие параллельно некоторой плоскости, называемой плоскостью поляризации прибора, и полностью задерживающие ортогональные колебания. Если пропустить через такой прибор пучок света, то на выходе он будет линейно поляризованным. При вращении прибора вокруг направления луча интенсивность выходящего света будет изменяться от I_MAX до I_MIN.

Отметим, что формула (6.4)  пригодна для расчета степени поляризации света лишь в том случае, когда частично поляризованный свет представляет собой смесь естественного света и света линейно поляризованного и не работает, например, в случае смеси естественного света и света поляризованного по кругу. В общем случае степень поляризации может быть рассчитана как отношение интенсивности поляризованной компоненты  к суммарной интенсивности волны, то есть сумме интенсивностей поляризованной  и естественной  компонент смеси:

 

Нетрудно показать, что (6.4) есть частный случай последней формулы.

Если падающий пучок света линейно поляризован, то при положении прибора, когда его плоскость поляризации ортогональна плоскости колебаний волны, свет через прибор не пройдет, то есть . В соответствии с формулой (6.4) степень поляризации такого света . Для частично поляризованного света

и . Для естественного света, где волны разных поляризаций смешаны в равной степени и все направления эквивалентны, интенсивность выходящего света не изменяется при вращении поляризатора, так что  и .

Закон Малюса. В качестве поляризаторов могут быть использованы среды, анизотропные в отношении колебаний вектора Е, например природные кристаллы турмалина. Монокристалл турмалина поглощает колебания вектора Е в одном направлении настолько сильно, что сквозь пластинку толщиной порядка 1 мм проходит только линейно поляризованный луч. Кристаллы йодистого хинина еще сильнее поглощают одну из поляризаций: кристаллическая пленка толщиной в десятую долю миллиметра практически полностью отделяет один из линейно поляризованных лучей.

Пусть естественный свет распространяется перпендикулярно плоскости рисунка 6.2.

Рис. 6.2. Разложение вектора амплитуды колебаний А в волне, падающей на поляризатор

Вектор  амплитуды колебаний электрического поля волны, совершающихся в плоскости, образующей с плоскостью поляризатора угол , можно разложить на два колебания с амплитудами

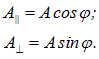
Первое колебание с амплитудой А_|| пройдет через прибор (поляризатор), второе — с амплитудой А — будет задержано (поглощено). Интенсивность прошедшей волны пропорциональна квадрату амплитуды

Падающая волна является смесью волн с различными углами . Усредняя по углам, получаем для интенсивности света на выходе из поляризатора:

где  — интенсивность падающего на поляризатор света. В естественном свете все значения угла  равновероятны:

так что интенсивность света, прошедшего через поляризатор, будет равна . При вращении поляризатора вокруг направления луча естественного света интенсивность прошедшего света остается неизменной, но изменяется лишь ориентация плоскости колебаний света, выходящего из прибора.

Рассмотрим теперь падение линейно поляризованного света с интенсивностью  на тот же поляризатор (рис. 6.3).

Рис. 6.3. Прохождение линейно поляризованной волны через поляризатор

Видео 6.1 Поляризатор и анализатор для дециметровой волны.

Видео 6.2 Поляризатор и анализатор для трехсантиметровой волны.

Сквозь прибор пройдет составляющая колебаний с амплитудой

где  — угол между плоскостью колебаний вектора Е и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением

которое носит название закона Малюса. 

Видео 6.3 Поляризатор и анализатор для видимого света — 2

Видео 6.4 Естественный видимый свет. Три поляризатора. Закон Малюса.

Поляризационные приборы по своему целевому назначению делятся на поляризаторы и анализаторы. Поляризаторы служат для получения поляризованного света. С помощью анализатора можно убедиться, что падающий свет поляризован, и выяснить направление плоскости поляризации. Принципиальных различий в конструкционном отношении между поляризатором и анализатором не существует.

Поставим на пути естественного света два поляризатора, плоскости которых образуют угол  (рис. 6.4).

Рис. 6.4. Пропускание естественного света через систему из двух поляризаторов

Из первого поляризатора выйдет линейно поляризованный свет, интенсивность которого , составит половину интенсивности падающего естественного света . Согласно закону Малюса из второго поляризатора (который играет роль анализатора) выйдет свет с интенсивностью

Таким образом, интенсивность света, прошедшего через два поляризатора, равна

Если угол  (плоскости поляризации поляризатора и анализатора параллельны), то ; если  (анализатор и поляризатор скрещены), то .

Пример 1. В частично поляризованном свете амплитуда колебаний, соответствующая максимальной интенсивности света при прохождении через поляризатор, в n = 2 раза больше амплитуды, соответствующей минимальной интенсивности. Определим степень поляризации света.

Поскольку интенсивность пропорциональна квадрату амплитуды, имеем

Отсюда степень поляризации света равна

Пример 2. На пути света со степенью поляризации Р = 0.6 поставили анализатор так, что интенсивность прошедшего света стала максимальной. Определим, во сколько раз уменьшится интенсивность, если анализатор повернуть на угол ?

В падающем луче по условию (см. предыдущий пример)

При повороте анализатора на угол  будут пропущены колебания, параллельные плоскости поляризации прибора. Поэтому интенсивность пропущенных колебаний, прежде бывших параллельными плоскости поляризации, составит

a интенсивность прошедших колебаний, до поворота задерживавшихся анализатором, равна

Суммарная интенсивность прошедших колебаний равна сумме

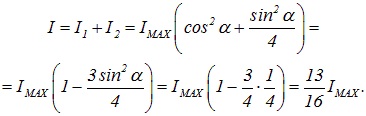
Стало быть, интенсивность уменьшится при повороте анализатора в 16/13 = 1.23 раза.

Поляризация при отражении и преломлении. Получить поляризованный свет из естественного можно еще одним способом — отражением. Опыт показывает, что отраженный от поверхности диэлектрика и преломленный лучи всегда частично поляризованы. Когда свет падает на диэлектрическую поверхность, то в отраженном луче преобладают колебания, перпендикулярные плоскости падения (точки на рис. 6.5), а в преломленном луче - колебания, параллельные плоскости падения (стрелки на рис. 6.5).

Рис. 6.5. Поляризация света при отражении и преломлении

Видео 6.5 Поляризация естественного света при отражении от стекла.

Степень поляризации зависит от угла падения лучей и от относительного показателя преломления сред. Исследуя это явление, английский физик Д. Брюстер установил, что при определенном значении угла падения

удовлетворяющем условию

отраженный свет полностью поляризован в плоскости, перпендикулярной плоскости падения луча. Это соотношение известно как закон Брюстера. При

отражается только та компонента вектора напряженности электрического поля, которая параллельна поверхности диэлектрика (перпендикулярна плоскости падения). Соответственно, преломленный луч всегда частично поляризован, так как отражается лишь какая-то доля падающего света (не равная 50 %).

Видео 6.6 Угол Брюстера.

Действительно, при

находим с учетом закона преломления

Получаем отсюда

Таким образом,

откуда следует, что преломленный луч 0С перпендикулярен отраженному лучу 0В (рис. 6.6).

Рис.6.6. Ход лучей при падении света под углом Брюстера: отраженный луч ортогонален преломленному,
 поэтому излучатели типа  (см. текст ниже) не вносят вклад в поляризацию отраженного луча 

Для того чтобы объяснить, почему отраженный при падении под углом Брюстера луч линейно поляризован в плоскости, перпендикулярной плоскости падения, учтем, что отраженный свет есть результат излучения вторичных волн колеблющимися под действием светового вектора волны электрическими зарядами (электронами) в среде II. Эти колебания происходят в направлении колебаний вектора Е.

Разложим колебания вектора Е в среде II на два взаимно перпендикулярных направления (см. рис. 6.6): колебания , происходящие в плоскости падения (показаны стрелками), и колебания , происходящие перпендикулярно плоскости падения (показаны точками). В случае падения под углом Брюстера

отраженный луч 0В перпендикулярен преломленному лучу 0С. Следовательно, 0В параллелен . Из электромагнитной теории Максвелла известно, что колеблющийся электрический заряд не излучает электромагнитных волн вдоль направления своего движения. Поэтому колеблющийся в диэлектрике излучатель типа  вдоль направления 0В не излучает. Таким образом, по направлению отраженного луча 0В распространяется свет, посылаемый только излучателями типа , направления колебаний которых перпендикулярны плоскости падения.

Следует отметить, что на опыте закон Брюстера не выполняется вполне строго из-за дисперсии света.

Пример 3. Определим, на какой угловой высоте над горизонтом должно находиться Солнце, чтобы солнечный свет, отраженный от поверхности воды, был полностью поляризован.

Угол падения света связан с высотой Солнца над горизонтом соотношением

По условию угол падения равен углу Брюстера, так что

Показатели преломления воды п₂ = 1.33, воздуха — п₁ = 1. Отсюда находим

Пример 4. Угол Брюстера при падении света из воздуха на кристалл каменной соли равен . Определим скорость света V в этом кристалле.

Поскольку показатель преломления воздуха равен единице, показатель преломления каменной соли п совпадает с относительным показателем преломления  этих двух сред. Имеем поэтому

Видео 6.7 Поляризация света при двойном лучепреломление на границе раздела с анизотропным (одноосным) кристаллом. 

 

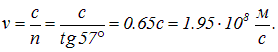
Дополнительные материалы

http://physbook.ru/index.php/Kvant... – Опыты и задачи по поляризации света

http://www.physics.spbstu.ru/forstudents/lectures/zaharov/20.pdf – Н.Г. Захаров. Практические занятия. Поляризация света

http://allphysics.ru/feynman/polyarizatsiya – Фейнмановские лекции по физике. Поляризация.

http://elementy.ru/trefil/21106 – Закон Брюстера.