1.5. Алгебра векторов

Как известно, бывают величины скалярные, не имеющие направления, а бывают векторные, которым кроме величины приписывается некое направление. Время — величина скалярная, а положение в пространстве надо задавать векторами. Недостаточно сказать, что лекция состоится в 860 км от Таллинна. Этой информации не хватит, чтобы узнать, где именно: в Москве или, скажем, в Копенгагене. Отсюда ясно, что векторы должны играть важную роль в физике. Недаром векторное исчисление получило современный вид именно благодаря работам физиков (Дж. Гиббс). Кроме длины и направления, для векторов определяются операция умножения вектора на действительное число и операция сложения векторов, то есть задается векторная алгебра.

Использование векторного исчисления удобно тем, что многие соотношения получаются в общем компактном виде и без особого труда могут быть трансформированы в соответствующие соотношения для любой системы координат. Соотношения между векторами остаются неизменными при смене начала отсчета или выборе иной системы координат. В этом разделе мы напомним некоторые правила векторной алгебры. Занимаясь сейчас физикой, мы не стремимся к точным математическим доказательствам.

Пусть нам дана какая-то декартова прямоугольная система координат. Любой вектор A можно задать тремя компонентами — проекциями вектора на оси , , .В дальнейшем мы используем обе общепринятых записи векторов, выделяя соответствующую букву жирным шрифтом, либо ставя над ней вектор:

Длина вектора не меняется при поворотах системы координат.

Отсюда следует, во-первых, что длина вектора B равна длине вектора A, умноженной на абсолютное значение числа

Во-вторых, векторы A и A коллинеарны и имеют одно направление, если >0, и противоположное, если <0.

Отсюда следует геометрическое представление суммы векторов — правило параллелограмма либо правило треугольника (рис. 1.12).

Рис. 1.12. Сложение двух векторов

Аналогично для вычитания векторов

где

Правило вычитания векторов иллюстрируется на рис. 1.13.

Рис. 1.13. Вычитание векторов

Единичный вектор n_A в направлении какого-то вектора а равен

Особую роль играют единичные векторы вдоль положительных направлений осей , , системы координат.

Иногда оси маркируются цифрами (1,2,3 ) или индексами соответствия осям (x,y,z) обозначают так

или

Любой вектор а можно представить в виде разложения по базису

На рис. 1.14 показано разложение вектора вдоль координатных осей

Рис. 1.14. Разложение вектора вдоль координатных осей

Отсюда следует, что скалярное произведение вектора на самого себя равно квадрату длины вектора

Второе следствие: скалярное произведение коммутативно, то есть

Справедливо также соотношение

Скалярное произведение не зависит от поворотов системы координат. Можно систему повернуть так, чтобы оба вектора лежали в плоскости и ось была направлена вдоль вектора а. В этой повернутой системе координат векторы-сомножители имеют следующие проекции:

Поэтому скалярное произведение может быть также представлено в виде

Здесь — угол между векторами а и b.

Если векторы ортогональны, то есть

то скалярное произведение равно нулю:

Обратно: если скалярное произведение равно нулю, то либо один из сомножителей — вектор нулевой длины, либо они ортогональны.

Рис. 1.15. Скалярное произведение

Приведем пример использования скалярного произведения (рис. 1.16). Пусть

Возведем в квадрат обе части равенства:

Это — так называемая теорема косинусов; в частном случае прямоугольного треугольника из нее следует теорема Пифагора.

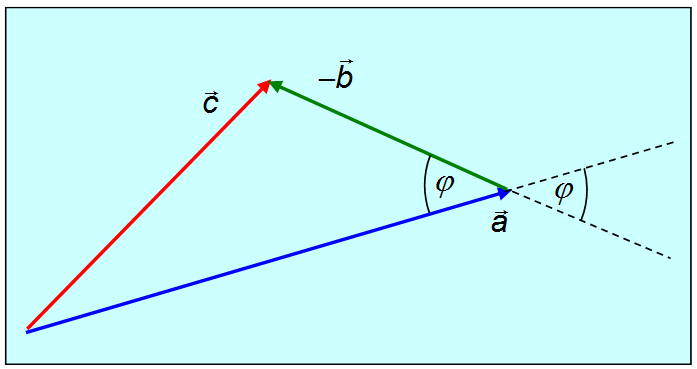
Рис. 1.16. Теорема косинусов

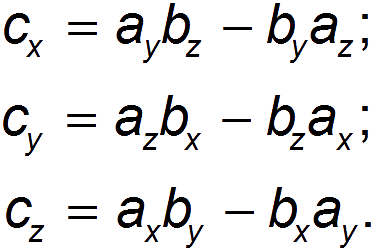
Отсюда следует, что разложение векторного произведения по базису может быть представлено в виде определителя

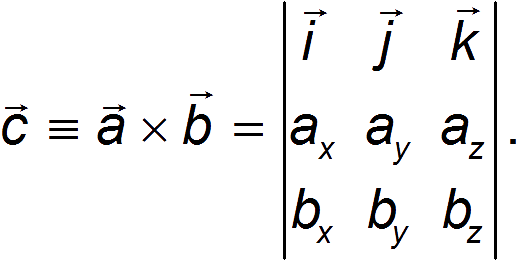
(1.5.1)

Для обозначения векторного произведения используется либо косой крест между сомножителями, либо помещение разделенных запятой (запятая необязательна, если и без неё ясно, где кончается первый сомножитель и начинается второй) сомножителей в квадратные скобки.

Видно также, что в векторном произведении важен порядок сомножителей

Справедливо соотношение

Чтобы понять, куда направлено векторное произведение и чему равна его длина, снова повернем систему координат так, чтобы плоскость осей совпала с плоскостью векторов а и b и ось была направлена вдоль вектора а. Тогда

Подставляя эти значения в определитель (1.5.1) для векторного произведения, получаем

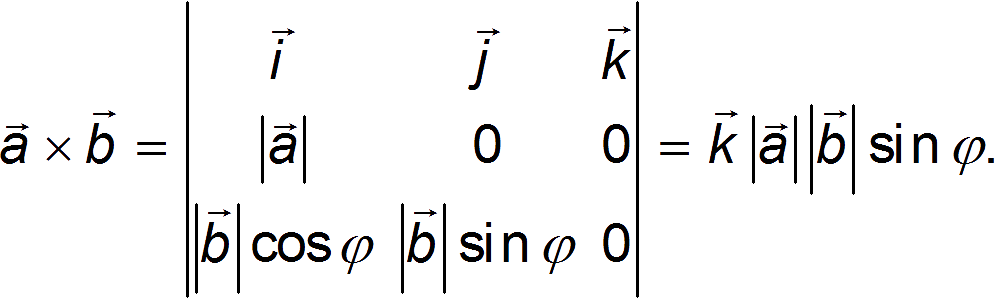
Это значит, что длина векторного произведения равна

и оно ортогонально обоим сомножителям а и b, причем направление его определяется по правилу правого винта.

Применение правила буравчика иллюстрируется на рис. 1.17.

Рис. 1.17. Правило буравчика для определения направления векторного произведения

Видео 1.2. Правое и левое вращение. Векторное произведение векторов

Если сомножители векторного произведения коллинеарны (, ; = 0), то векторное произведение равно нулю. Обратно, из равенства нулю векторного произведения вытекает, что либо векторы — сомножители коллинеарны, либо один из векторов равен нулю.

Пусть, например, вектор а зависит от времени t. Тогда

Производные от скалярного и векторного произведений выглядят обычным образом:

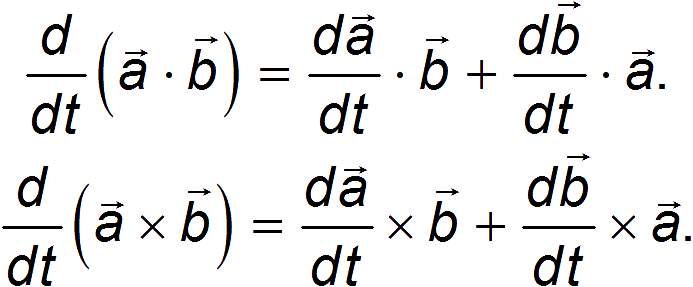
Подчеркнем, что в выражении для производной векторного произведения необходимо сохранять исходный порядок сомножителей.

Дополнительная информация

http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г.– стр. 54–59 (§ 7, п.п.9–11 и задачи 1–4): о векторных и скалярных величинах в физике.

http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г.– стр. 44–48 (§ 6): о смысле производной и интеграла в физических приложениях.