8.2. Силы инерции при ускоренном поступательном движении системы отсчета

Рассмотрим шарик, подвешенный на нити, точка подвеса которого 0' движется с ускорением a относительно некоторой инерциальной системы отсчета К. Нить подвеса отклоняется от вертикали на некоторый угол . Угол этот таков, чтобы равнодействующая F силы натяжения нити T и силы тяжести mg привела к движению шарика с ускорением a:

откуда

Так выглядит описание явления с точки зрения наблюдателя в инерциальной системе отсчета К (рис. 8.1).

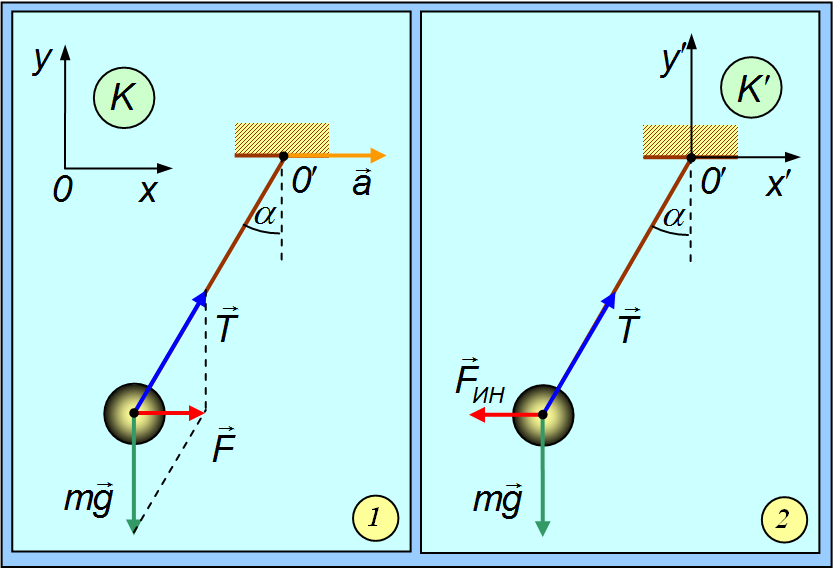
Рис. 8.1. Движение шарика на нити, точка подвеса которого движется с ускорением: 1 — с точки зрения наблюдателя в инерциальной системе отсчета; 2 — с точки зрения наблюдателя в движущейся неинерциальной системе отсчета

Свяжем теперь систему отсчета К' с точкой подвеса 0'. Эта система будет неинерциальной, так как она движется с ускорением a относительно инерциальной системы К. Мы пользуемся нерелятивистской механикой, так что угол отклонения нити, равно как и силы T, mg для обоих наблюдателей одинаковы. Но для наблюдателя К' шарик находится в покое (см. рис. 1–2) С другой стороны, наблюдатель К' видит, что результирующая сил T и mg не равна нулю. Поэтому наблюдатель К' приходит к выводу, что в его системе отсчета действует какая-то сила — сила инерции , которой не было в инерциальной системе отсчета К. Выражение для силы инерции получаем из условия равновесия шарика в системе К', то есть из равенства нулю трех сил:

Отсюда

и из уравнения второго закона Ньютона для тела следует выражение для силы инерции при поступательном движении неинерциальной системы отсчета с ускорением a:

Этот же результат верен в общем случае для произвольного движения материальной точки в движущейся поступательно неинерциальной системе отсчета К'. Пусть скорость ее движения относительно инерциальной системы отсчета К описывается функцией , а оси обеих систем остаются параллельными. Пусть скорость движения материальной точки в системе К меняется по закону . Значит, в инерциальной системе К согласно второму закону Ньютона на точку действует сила

Скорость этой же точки для наблюдателя в системе К' равна

Значит в неинерциальной системе отсчета К' на точку действует сила

Таким образом, и в этом случае сила инерции определяется формулой

где — ускорение поступательного движения неинерциальной системы относительно инерциальной.

Видео 8.3. Маятник на тележке ускоренно скатывающейся с наклонной плоскости

Заметим, что благодаря равенству гравитационной и инертной масс, обсуждавшемуся в главе 5.4, наблюдатель в системе К' может утверждать, что в его системе имеется однородное гравитационное поле, заставляющее тела «падать» с ускорением

Эйнштейн сформулировал принцип эквивалентности неинерциальных систем и гравитационных полей и построил на этой основе общую теорию относительности (ОТО) или теорию гравитации.

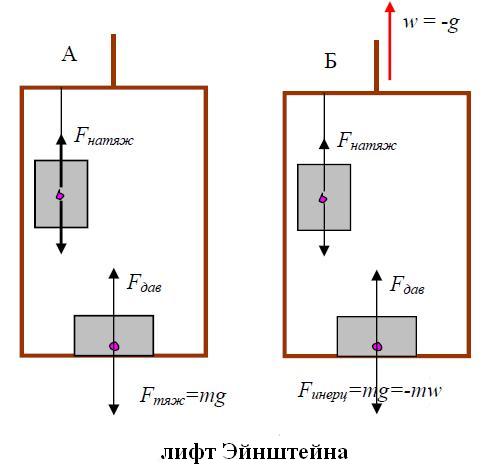
Рис. 8.2. Лифт Эйнштейна

Возникновение силы инерции при поступательном ускоренном движении системы отсчета демонстрируется в опыте, показанном на рис. 8.2.