ГЛАВА 12. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ. КИНЕМАТИКА И ДИНАМИКА
Природа же этой силы может быть различной в разных задачах: в рассмотренном примере – это сила трения, при вращении груза на веревке – сил натяжения и т.д.
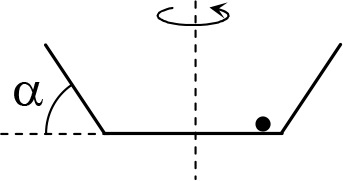
Рис. 12.8
Пример 12.5. Сосуд, имеющий форму расширяющего усеченного конуса с радиусом дна R и углом наклона стенок α, вращается вокруг вертикальной оси. При какой угловой скорости вращения сосуда ω маленький шарик, лежащий на его дне (рис. 12.8), будет выброшен из сосуда? Трение мало. Какая сила выбрасывает шарик из сосуда?
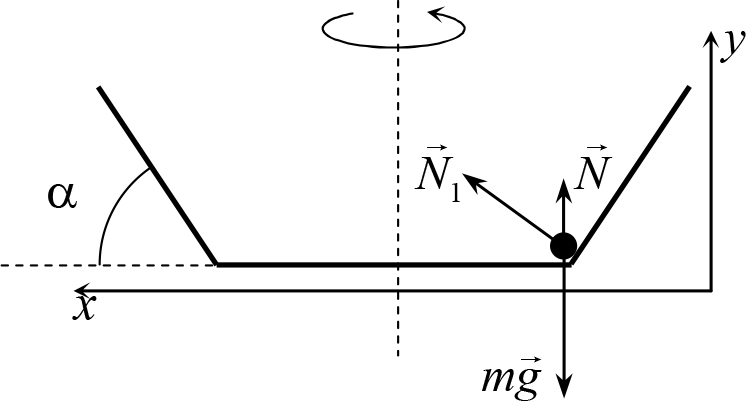
Рис. 12.9
Решение. Силы, действующие на шарик, показаны на рис. 12.9. Здесь ![]() – сила тяжести,
– сила тяжести, ![]() – сила реакции дна сосуда,
– сила реакции дна сосуда, ![]() – сила реакции боковой стенки (силы реакции перпендикулярны соответствующим поверхностям). Второй закон Ньютона дает
– сила реакции боковой стенки (силы реакции перпендикулярны соответствующим поверхностям). Второй закон Ньютона дает
![]()
Проецируя второй закон Ньютона на оси x и y, показанные на рис. 12.9, и учитывая, что ускорение тела направлено горизонтально к центру сосуда и равно ω2R, получим
![]()
Выражая силу реакции N1 из первого уравнения и подставляя это выражение во второе уравнение, найдем силу N как функцию угловой скорости вращения сосуда
![]()


