ГЛАВА 18. ГАЗОВЫЕ ЗАКОНЫ
С учетом этого выражения уравнение (18.10) (которое называют еще уравнением состояния идеального газа) можно записать в следующих, эквивалентных (18.10), формах:
Уравнение Клапейрона-Менделеева (18.10) или (18.12) позволяет находить один неизвестный макроскопический параметр газа (например, давление p) по известным трем другим (объему V, температуре T и числу молей ![]() ). Или какие-то величины, связанные с входящими в уравнение состояния — плотность, молярную массу и др. Если при этом сосуд, в котором находится газ, имеет подвижные стенки, или ограничивается подвижным поршнем, то давление газа в случае равновесия таких стенок или поршня может быть найдено механически из условия равновесия этих стенок или поршня. В этом случае достаточно задать только два параметра (например, объем V и число молекул N), чтобы определить все остальные: давление p — из условия равновесия поршня, а затем температуру газа T — по известным p, V и N из уравнения состояния. Рассмотрим несколько примеров.
). Или какие-то величины, связанные с входящими в уравнение состояния — плотность, молярную массу и др. Если при этом сосуд, в котором находится газ, имеет подвижные стенки, или ограничивается подвижным поршнем, то давление газа в случае равновесия таких стенок или поршня может быть найдено механически из условия равновесия этих стенок или поршня. В этом случае достаточно задать только два параметра (например, объем V и число молекул N), чтобы определить все остальные: давление p — из условия равновесия поршня, а затем температуру газа T — по известным p, V и N из уравнения состояния. Рассмотрим несколько примеров.
Пример 18.2. В цилиндрическом сосуде площадью поперечного сечения S под подвижным поршнем массой m находится некоторый идеальный газ в количестве ![]() молей. Определить температуру газа, если в равновесии поршень расположен на высоте h от дна сосуда. Атмосферное давление
молей. Определить температуру газа, если в равновесии поршень расположен на высоте h от дна сосуда. Атмосферное давление ![]() .
.
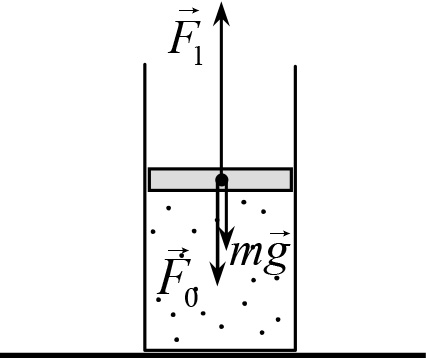
Рис. 18.1
Решение. Для того чтобы найти температуру газа с помощью уравнения Клапейрона-Менделеева необходимо знать объем газа (который нам здесь, фактически, известен), число молей (которое также известно) и давление газа p. Давление газа нам неизвестно, однако в условии сказано, что сосуд ограничен подвижным поршнем, который находится в равновесии. Используем условие равновесия поршня, чтобы найти давление газа.


