ГЛАВА 24. НАПРЯЖЕННОСТЬ И ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Действительно, пусть заряд q перемещается из некоторой точки 1 в некоторую точку 2 электрического поля. Поскольку работа поля не зависит от траектории, для вычисления работы поля ![]() рассмотрим вспомогательную траекторию 1→O→2 (см. рис. 24.8)
рассмотрим вспомогательную траекторию 1→O→2 (см. рис. 24.8)
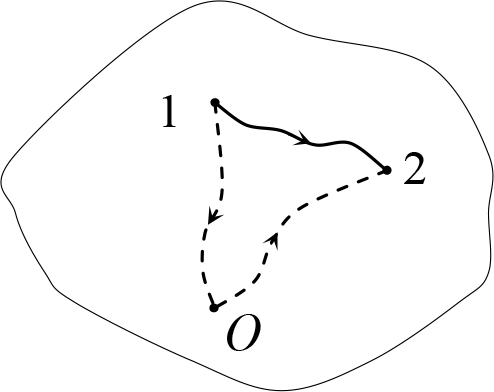
Рис. 24.8
Из определения потенциала (24.13) имеем ![]() , где
, где ![]() - потенциал поля в точке 1. Очевидно,
- потенциал поля в точке 1. Очевидно, ![]() . Это связано с тем, что при изменении направления движения заряда меняется знак косинуса угла между векторами силы и перемещения на каждом элементарном участке перемещения заряда. Поэтому
. Это связано с тем, что при изменении направления движения заряда меняется знак косинуса угла между векторами силы и перемещения на каждом элементарном участке перемещения заряда. Поэтому ![]() (
(![]() - потенциал поля в точке 2), и из формулы (24.14) получаем для работы поля над зарядом при его перемещении из точки 1 в точку 2
- потенциал поля в точке 2), и из формулы (24.14) получаем для работы поля над зарядом при его перемещении из точки 1 в точку 2
т.е. работа поля над заряженным телом равна произведению его заряда на разность потенциалов начальной и конечной точек траектории (именно в такой последовательности).
Таким образом, знание потенциалов полей позволяет находить работу, которую совершают эти поля над движущимися в них зарядами. Однако вычисление потенциалов, как правило, представляет собой серьезную математическую проблему, для решения которой необходима высшая математика. Тем не менее потенциалы поля точечного заряда и сферы (а только с ними могут столкнуться школьники) вычислены, эти формулы нужно запомнить и использовать вместе с принципом суперпозиции для вычисления работ. Приведем основные формулы для потенциалов.
Поле точечного заряда. Выбираем начало отсчета потенциала в бесконечно удаленной точке. Тогда потенциал точки поля, лежащей на расстоянии r от заряда Q, равен
причем в формулу (24.16) входит заряд Q со «своим знаком» (не модуль). Другими словами, если заряд Q, создающий поле, отрицателен, то потенциал его поля отрицателен в каждой точке.


