ГЛАВА 3. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ. ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ

6. Корабль движется на запад со скоростью v₀ = 5 м/c. Ветер дует с юго-запада под углом α = 45° к меридиану. Направление скорости ветра, измеренной на палубе, составило угол β =150° с направлением скорости корабля. Определить скорость ветра относительно земли и относительно корабля.

7. Корабль движется на запад со скоростью v. Ветер дует с югозапада под углом α к меридиану. Скорость ветра, измеренная на корабле равна u. Найти скорость ветра относительно земли.

8. Поезд движется со скоростью v, при этом пассажиру кажется, что скорость ветра v₁.

Когда поезд увеличил скорость в два раза, сохранив направление движения, пассажиру кажется, что скорость ветра v₂. Определить скорость ветра относительно земли.

9. Самолет движется между городами A и B и обратно. Скорость самолета относительно воздуха равна v. Под некоторым углом α к направлению AB дует ветер. Скорость ветра равна u. При каком значении α время движения самолета туда и обратно минимально? Найти это время. Расстояние между городами l.

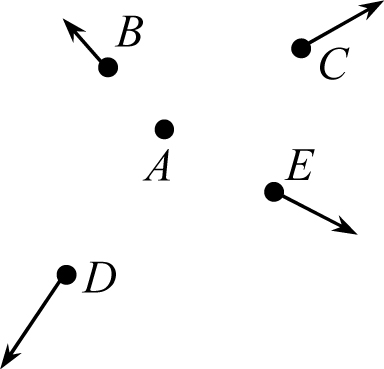
10. В некоторой планетной системе имеет место такая картина движения планет. Астрономы планеты А видят, что все планеты этой системы удаляются от планеты А со скоростями, пропорциональными их расстоянию до А, т. е. v_X = Hr_X.A, где v_X – скорость планеты X; r_X.A – расстояние между планетами Х и А, H – коэффициент пропорциональности, одинаковый для всех планет. Что видят астрономы других планет?