ГЛАВА 4. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
Так как v2 > v1, вектор изменения скорости Δ![]() =
= ![]() 2 −
2 − ![]() 1 за любой интервал времени Δt направлен вертикально вниз (вычитание векторов выполнено на правой части рисунка, вектор изменения скорости Δ
1 за любой интервал времени Δt направлен вертикально вниз (вычитание векторов выполнено на правой части рисунка, вектор изменения скорости Δ![]() выделен жирным). Поэтому и вектор мгновенного ускорения тела в рассматриваемой точке направлен вертикально вниз. А поскольку рассматриваемая точка траектории произвольна, то вектор мгновенного ускорения тела в любой точке при его свободном падении направлен вертикально вниз.
выделен жирным). Поэтому и вектор мгновенного ускорения тела в рассматриваемой точке направлен вертикально вниз. А поскольку рассматриваемая точка траектории произвольна, то вектор мгновенного ускорения тела в любой точке при его свободном падении направлен вертикально вниз.
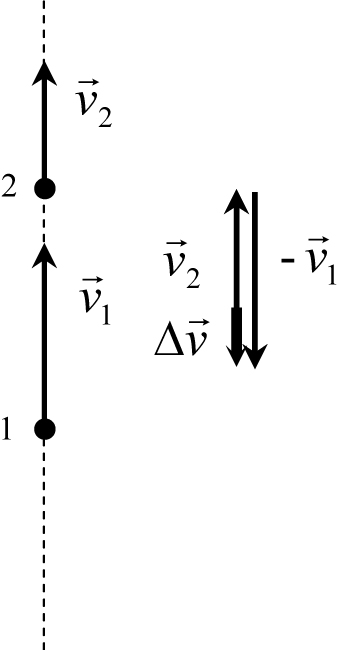
Рис. 4.2
При движении тела вертикально вверх, вектор его ускорения также направлен вниз. Действительно при таком движении скорость тела уменьшается по величине, поэтому вектор изменения скорости за любой малый интервал времени, и, следовательно, мгновенного ускорения направлен вниз (рис. 4.2; вектор изменения скорости Δ![]() =
= ![]() 2 −
2 − ![]() 1 выделен жирным).
1 выделен жирным).
Определим направление вектора мгновенного ускорения тела при криволинейном движении. Пусть тело, двигаясь по кривой траектории, в некоторый момент времени имеет скорость ![]() 1, а спустя малый интервал времени – скорость
1, а спустя малый интервал времени – скорость ![]() 2. На рис. 4.3 показан пример такой траектории, и два положения – 1 и 2 – движущегося тела.
2. На рис. 4.3 показан пример такой траектории, и два положения – 1 и 2 – движущегося тела.
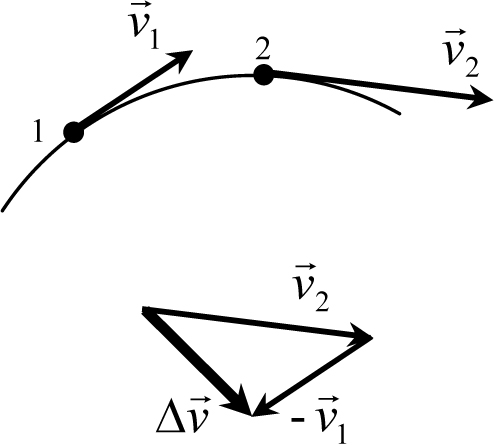
Рис. 4.3
Вычитая векторы скорости (нижняя вставка на рисунке), находим, что вектор изменения скорости, который выделен на рис. 4.3 жирным, а, следовательно, и ускорения тела направлен «внутрь» траектории под некоторым углом к вектору скорости. Этот угол зависит от того, увеличивается вектор скорости тела по величине, или уменьшается. Если величина скорости не изменяется, то треугольник вычитания скоростей равнобедренный, и вектор изменения скорости тела за малый интервал времени перпендикулярен вектору скорости.


