ГЛАВА 4. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

Поэтому, нам кажется, что для обозначения замедленного движения с постоянным ускорением также лучше использовать термин «равноускоренное движение».

Можно доказать, что при равноускоренном движении радиус-вектор тела по отношению к произвольной системе координат и его скорость следующим образом зависят от времени¹:

(4.2)

где (t) и (t) – радиус-вектор тела и его скорость как функции времени t. Время t в уравнениях (4.2) отсчитывается от некоторого момента, который мы называем начальным и которому отвечает t = 0, ₀ и ₀ – радиус-вектор и скорость тела в начальный момент (при t = 0), – ускорение. Начальный момент для уравнений (4.2) может быть выбран любым. При этом ₀ и ₀ – радиус-вектор и скорость тела именно в тот момент, который принят за начальный.

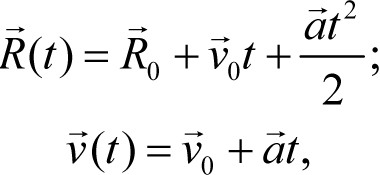
Уравнения (4.2) представляют собой зависимости радиус-вектора и скорости тела от времени, и потому вопрос «чему равно время в этих уравнениях» настолько же некорректен, как, например, вопрос «чему равен x в уравнении функции y = kx + b». Чему угодно! Время t в этих уравнениях – это переменная. Это значит, что подстановка любого значения времени в правую часть уравнений (4.2) и выполнение соответствующих действий с векторами позволяет найти радиус-вектор тела и его скорость в этот момент. Например, для заданных начальных значений радиус-вектора, начальной скорости и ускорения тела (рис. 4.4, а), радиус-вектор этого тела в момент времени t = 1 с и его скорость в этот момент находятся с помощью уравнений (4.2)

(4.3)

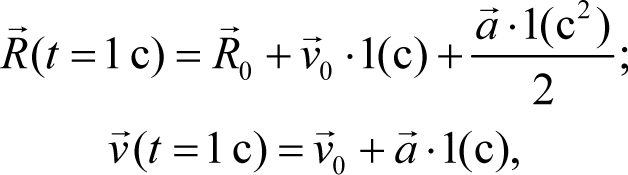
¹ Уравнения (4.2) можно строго вывести из определения ускорения. Этот вывод, однако, не входит в школьную программу по физике, и потому мы его здесь не рассматриваем. Первым уравнения (4.2), фактически, получил Галилей, предположив, что скорость возрастает пропорционально времени, а путь – квадрату времени.