Вариант 2.

Задача 17.2.1. 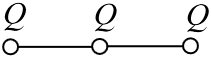Три шарика, заряженные одинаковыми зарядами 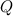расположены вдоль одной прямой и связаны нерастяжимыми нитями длиной 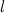. Найти силы натяжения нитей. ().

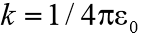Задача 17.2.2. 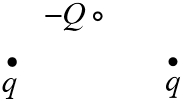Как направлена сила, действующая на отрицательный точечный заряд 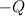со стороны двух одинаковых положительных точечных зарядов 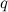(см. рисунок: заряд 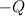расположен на перпендикуляре, проходящем через середину отрезка 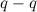)? 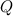, 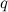> 0.

Задача 17.2.3. 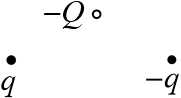Как направлена сила, действующая на отрицательный заряд 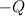со стороны двух точечных зарядов 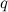и 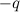(см. рисунок: заряд 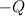расположен на перпендикуляре, проходящем через середину отрезка 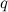(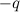) )? 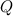, 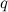> 0.

Задача 17.2.4. Три одинаковых точечных заряда 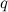расположены в вершинах равностороннего треугольника со стороной . Какая сила действует на каждый из них со стороны двух других?

Задача 17.2.5. 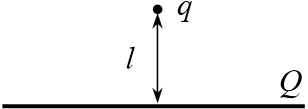Точечный заряд 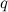расположен на расстоянии 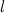от очень большой пластины, равномерно заряженной зарядом 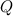. Чему равна сила взаимодействия между пластиной и зарядом? Площадь пластины — .

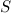Задача 17.2.6. 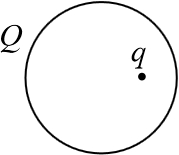Точечный заряд 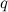находится внутри сферы с радиусом 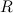, равномерно заряженной по поверхности зарядом 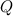. Расстояние от заряда до центра сферы равно 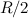(см. рисунок). Какая сила действует на точечный заряд со стороны сферы? ().

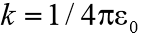Задача 17.2.7. 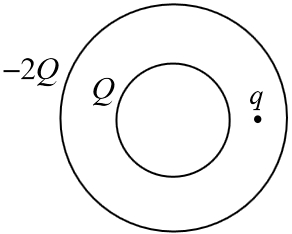Имеются две концентрические сферы с радиусам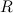и и 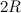, заряженные зарядам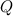и и 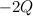( 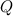> 0). На расстоянии 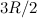от центра сфер находится положительный точечный заряд 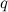(см. рисунок). Какая сила действует на заряд 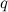со стороны сфер? ().

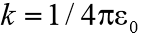Задача 17.2.8. Имеется два точечных заряда 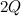и 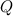( 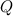> 0). В какой из показанных на рисунке точек — 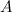, 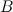или 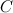— сила, действующая со стороны этих зарядов на некоторый помещенный в эту точку положительный заряд, будет наибольшей? Расстояния 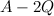, , 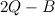, 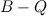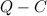— одинаковы.

Задача 17.2.9. Два одинаковых металлических шарика, заряженных зарядами одного знака, находятся на расстоянии, много большем их размеров. Шарики приводят в соприкосновение, а затем разводят на первоначальное расстояние. Что можно сказать о величине силы взаимодействия шариков?

Задача 17.2.10. Два одинаковых металлических шарика, заряженных зарядами противоположных знаков, находятся на расстоянии, много большем их размеров. Шарики приводят в соприкосновение, а затем разводят на первоначальное расстояние. Что можно сказать о величине силы взаимодействия шариков?