Вариант 1.

Задача 8.1.1. При увеличении в 3 раза расстояния между точечными телами сила их гравитационного притяжения

Задача 8.1.2. Как изменится сила взаимодействия двух точечных тел, если при неизменном расстоянии между ними массу одного увеличить в 2 раза, массу второго увеличить в 3 раза?

Задача 8.1.3. Как изменится сила взаимодействия двух точечных тел, если массу одного тела увеличить в два раза, второго — в четыре раза, а расстояние между телами — в восемь раз?

Задача 8.1.4. На каком расстоянии от центра Земли ускорение свободного падения составляет половину ускорения свободного падения на ее поверхности? Радиус Земли .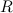

Задача 8.1.5. Определить ускорение свободного падения на поверхности Марса, если масса Марса приблизительно в 10 раз меньше массы Земли, а радиус приблизительно в 2 раза меньше радиуса Земли. Считать, что ускорение свободного падения на поверхности Земли 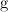= м/с².

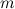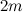Задача 8.1.6. Два точечных тела с массами и удерживают на некотором расстоянии друг от друга. Тела одновременно отпускают. Сравнить ускорения тел. Тела взаимодействуют по закону всемирного тяготения.

Задача 8.1.7. Известно, что масса Меркурия составляет 1/18 массы Земли, а расстояние от Меркурия до Солнца в 2,5 раза меньше расстояния от Земли до Солнца. Во сколько раз сила притяжения Земли к Солнцу больше силы притяжения Меркурия к Солнцу?

Задача 8.1.8. Ракета удаляется от земли. На каком расстоянии от поверхности земли сила гравитационного притяжения ракеты к земле уменьшается в 4 раза по сравнению с силой притяжения на поверхности?

Задача 8.1.9. 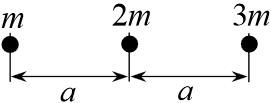Три точечных тела с массам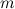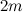и , и 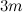расположены на одной прямой на одинаковых расстояниях друг от друга (см. рисунок). Чему равна сила, действующая на центральное тело?

Задача 8.1.10. 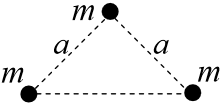Три точечных тела массой 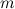каждое расположены в вершинах равнобедренного прямоугольного треугольника с катетами, равными (см. рисунок). Чему равна сила, действующая на тело, находящееся в вершине прямого угла?