Глава 10. Статика

Статика — это раздел динамики, в котором рассматривается равновесие тел, и формулируются условия, при выполнении которых тела находятся в равновесии. Для успешного решения задач «на статику» необходимо уметь вычислять моменты сил, знать и уметь использовать условия равновесия тел. При этом следует помнить, что при вычислении моментов распределенных сил (тяжести, трения, реакции) возникает понятие центра тяжести тела, как точки, к которой надо приложить суммарную распределенную силу для вычисления ее момента.

Момент силы определяется по отношению к некоторой точке, которую будем называть началом отсчета моментов, и которая выбирается произвольно. Моментом силы называется произведение модуля силы на ее «плечо» , которое определяется как длина перпендикуляра, опущенного из начала отсчета момента на прямую, вдоль которой действует сила

(10.1)

Например, плечом силы относительно точки (см. рисунок) является отрезок . Знак момента определяется следующим образом. Надо представить, что через точку проходит ось вращения тела, на которое действует сила . Если сила стремится закрутить тело по часовой стрелке относительно этой оси, то момент силы отрицателен, если против часовой стрелки — положителен. (Следует иметь в виду, что знак момента можно было выбирать и наоборот. Дело в том, что момент силы — это вектор. В школьном курсе, однако, определение вектора момент не вводится, и рассматриваются только такие ситуации, когда векторы момента направлены вдоль одной оси. Данное выше определение момента — это определение проекции вектора момента на эту ось. А поскольку направление оси никак не определяется, то важен только относительный знак проекций момента.) Из определения момента (10.1) следует, что момент силы равняется нулю, если прямая, вдоль которой она действует, проходит через начало отсчета момента.

Если на неточечное тело действуют силы, у которых нет определенной точки приложения, например, сила тяжести, сила трения, сила реакции (такие силы принято называть распределенными), то для вычисления их моментов можно поступить следующим образом. Необходимо разбить это тело на бесконечно малые элементы, вычислить момент силы, действующей на каждый элемент, просуммировать полученные моменты. Оказывается, что если распределенные силы пропорциональны массам элементов и одинаково направлены, для вычисления момента распределенной силы нужно суммарную распределенную силу приложить к некоторой точке, которая называется центром тяжести тела. Центр тяжести тела, обладающего центральной симметрией (а только такие тела и могут встретиться школьникам), находится в геометрическом центре тела.

Тело находится в равновесии по отношению к инерциальной системе отсчета, если сумма всех сил, действующих на тело, равна нулю

(10.2)

и сумма моментов этих сил, вычисленных относительно произвольного начала отсчета, равна нулю

(10.3)

Условия (10.2), (10.3) можно использовать для определения сил, действующих на тело, которое находится в равновесии.

В задаче 10.1.1 начало отсчета моментов (точка ) лежит на линии действия силы . Поэтому момент этой силы относительно точки равен нулю (ответ 3).

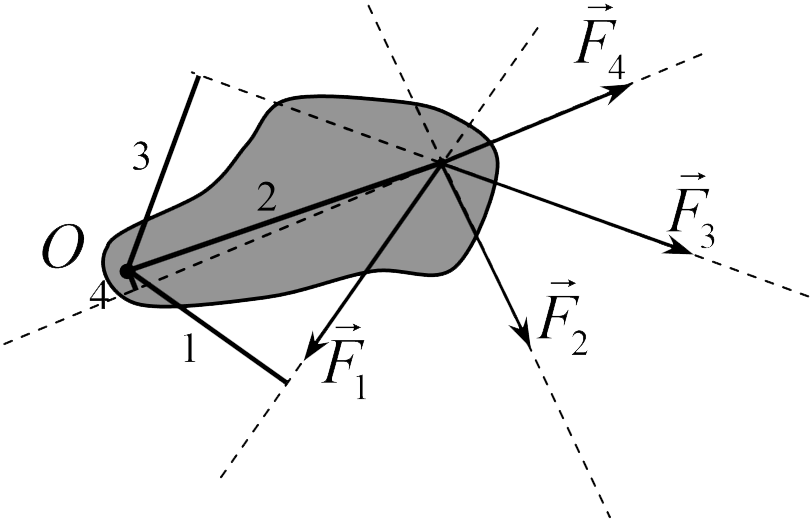
На рисунке числами 1, 2, 3 и 4 отмечены отрезки (толстые сплошные линии), которые представляют собой плечи сил , , или (задача 10.1.2) относительно точки (линии действия сил показаны тонким пунктиром). Из этого рисунка видим, что из этих сил наибольшее плечо имеет сила (правильный ответ в этой задаче – 2).

Для момента первой силы из задачи 10.1.3 имеем

Тогда для момента второй силы получаем

т.е. момент второй силы в раз больше момента первой силы (ответ 1).

По определению плечо силы — это перпендикуляр опущенный из начала отсчета момента (точки в задаче 10.1.4) на линию действия силы. Поэтому плечо силы реакции — отрезок (или , который равен отрезку ). Следовательно, плечо силы реакции вертикальной стенки, действующей на лестницу, равно длине отрезка . Правильный ответ в задаче – 1.

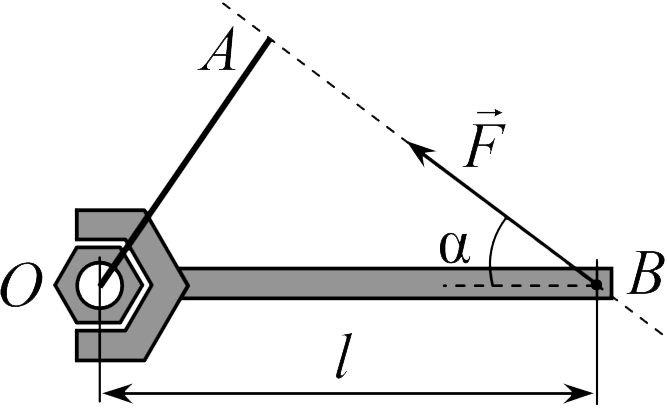
Плечо силы в задаче 10.1.5 равно отрезку (см. рисунок). Из прямоугольного треугольника получаем для плеча силы — . Поэтому момент силы равен

(ответ 1).

На тело массой , находящееся на наклонной плоскости с углом наклона (задача 10.1.6), со стороны плоскости действует сила реакции, направленная перпендикулярно плоскости и равная . Поэтому момент этой силы относительно основания плоскости длиной (см. рисунок в условии задачи) равен (ответ 2).

Чтобы рычаг был в равновесии сумма моментов всех сил, действующих на рычаг, должна равняться нулю, причем относительно любой точки — начала отсчета моментов. На рычаг в задаче 10.1.7 действуют: сила 3 Н на плечо длиной 0,1 м, искомая сила — на плечо длиной 0,3 м и сила со стороны оси вращения. Помещая начало отсчета моментов на оси вращения и находя моменты сил, действующих на плечи рычага, получаем из условия равновесия (10.3)

(момент силы, действующей на рычаг со стороны оси вращения равен нулю относительно выбранного начала). Отсюда находим, что (ответ 1).

Ось вращения стержня в задаче 10.1.8 надо расположить в такой точке, чтобы сумма моментов сил и относительно этой оси равнялась бы нулю. При этом очевидно, что ось должна располагаться справа от точки приложения силы . Поскольку величина силы втрое больше величины силы , то плечо силы должно быть втрое меньше плеча силы . Поэтому правильный ответ в задаче — 4.

Приравнивая величины моментов сил тяжести, действующих на тела, относительно опоры (задача 10.1.9), получим

где — расстояние от опоры до левого груза. Отсюда находим (ответ 2). Аналогично в задаче 10.1.10 получим (ответ 4).

В задаче 10.2.1 на невесомый стержень действуют две силы натяжения нитей и , и сила со стороны груза, равная его силе тяжести (см. рисунок). Используем условие равновесия стержня (10.3). Моменты удобно вычислять относительно начала отсчета , помещенного около правого конца стержня. Относительно этого начала имеем , , (здесь использовано, что точка крепления груза делит стержень в отношении 1:3). Поэтому из условия (10.3) получаем . Отсюда 4 кг (ответ 4).

Из условия равенства моментов, вращающих рычаг в задаче 10.2.2 по и против часовой стрелки, получаем (ответ 4).

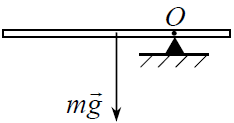
Как отмечалось во введении к настоящей главе, для нахождения момента распределенной силы (в данном случае момента силы тяжести) нужно силу тяжести, действующую на весь стержень, «приложить» к геометрическому центру стержня (к его середине) и вычислять момент этой силы так, как будто бы она является сосредоточенной (см. рисунок). Поэтому плечо силы тяжести относительно точки в задаче 10.2.3 равно — длина стержня), и момент силы тяжести относительно точки равен — ответ 3. Здесь — масса стержня.

Используя это значение момента силы тяжести, можно найти силу натяжения нити в задаче 10.2.4. Условие равновесия (10.3) относительно точки дает

где — момент силы натяжения относительно точки . Отсюда находим (ответ 3).

С одной стороны, если к стержню приложена минимальная необходимая для переворота сила (задача 10.2.5), сила реакции, действующая на стержень со стороны стола, будет приложена к точке, находящейся над самым краем. С другой стороны, если к концу стержня приложена именно такая сила, стержень практически находится в равновесии. Поэтому в том случае, когда на тело действует минимальная необходимая для переворота сила, сумма моментов силы тяжести и искомой силы относительно края стола равна нулю

Отсюда находим (ответ 2).

На стержень из задачи 10.2.6 действуют сила тяжести , реакции стенки и пола , а также сила трения со стороны пола, направленная так, как показано на рисунке, причем сила тяжести приложена к середине стержня. Используем условие равенства нулю суммы моментов внешних сил (10.3) относительно нижней точки стержня. Поскольку моменты силы трения и силы реакции относительно нижней точки стержня равны нулю, условие (10.3) дает

где — угол между стержнем и горизонтальной поверхностью (отмечен на рисунке дугой). Отсюда находим

Поскольку для рассматриваемого случая , , то (ответ 1).

При приложении к концу стержня минимально необходимой для отрыва этого конца от поверхности (задача 10.2.7) силы одновременно выполнены два следующих условия. Поскольку стержень 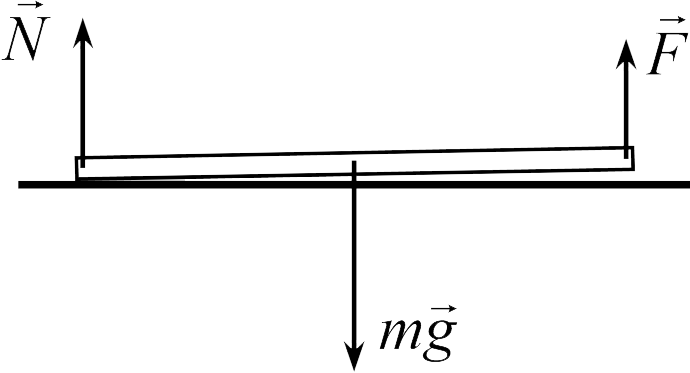практически находится в равновесии, то еще выполнены уравнения статики — сумма моментов сил, действующих на стержень, равна нулю. С другой стороны, в этот момент стержень уже начинает отрываться от поверхности, и сила реакции опоры будет приложена к другому концу стержня (см. рисунок). Поэтому сумма моментов силы и силы тяжести относительно левого конца стержня должна равняться нулю . Отсюда (ответ 4).

При приложении к бруску минимально необходимой для его переворота силы (задача 10.2.8) сумма моментов сил тяжести и относительно упора (см. рисунок в условии) равна нулю. Этот вывод обосновывается так же, как и в предыдущей задаче. Поэтому (ответ 3).

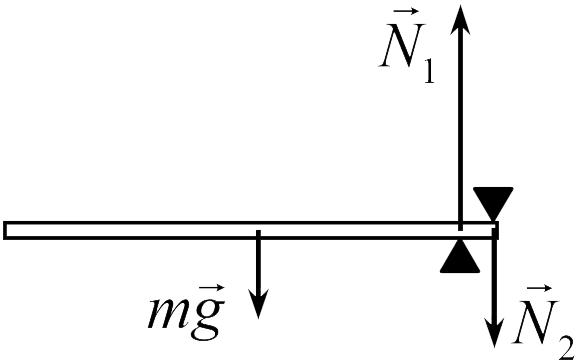
В задаче 10.2.9 проще всего сравнить силы реакции упоров, из условия равенства нулю суммы всех сил, действующих на стержень (формула (10.2)). На стержень действуют три силы: тяжести , и две силы реакции и (см. рисунок), сумма которых равна нулю, или . Поэтому сила реакции нижнего упора больше, чем верхнего (ответ 2).

Треугольник в задаче 10.2.10 находится в равновесии, если его центр тяжести лежит на вертикальной прямой, проходящей через шарнир. Это связано с тем, что на треугольник действуют две силы — тяжести и реакции шарнира — и, чтобы выполнялось условие моментов относительно шарнира, момент силы тяжести относительно шарнира должен равняться нулю. Докажем, что центр тяжести треугольника лежит в точке пересечения его медиан. Действительно, если разбить треугольник на тонкие полоски, параллельные одной из сторон, то центр тяжести каждой из них лежит в ее середине. Поэтому и центры тяжести всех полосок (а, значит, и всего треугольника) лежат на его медиане (см. рисунок; медиана показана пунктиром). А поскольку треугольник можно разделить на слои, параллельные второй и третьей его стороне, то центр тяжести лежит и на этих медианах, т.е. в точке их пересечения (правильный ответ 1).