Глава 14. Термодинамика

Изучение энергетических превращений в молекулярных системах составляет содержание термодинамики. Для решения задач на термодинамику необходимо знать определения внутренней энергии, количества теплоты, теплоемкости и ряда других величин. Необходимо также понимать и уметь использовать в простейших случаях первый закон термодинамики как балансовое соотношение, описывающее процессы превращения энергии из одних форм в другие. Также нужно знать основные свойства процессов перехода вещества из одних агрегатных состояний в другие. Рассмотрим эти вопросы.

Внутренней энергией тела называется сумма кинетической энергии молекул и потенциальной энергии их взаимодействия друг с другом. Для жидкостей и твердых тел из-за сильного взаимодействия молекул друг с другом вычислить внутреннюю энергию не удается. Внутреннюю энергию можно вычислить только для идеальных газов, в которых можно пренебречь энергией взаимодействия молекул друг с другом и считать, что внутренняя энергия равна сумме кинетических энергий молекул. Для одноатомного газа (т.е. газа, каждая молекула которого состоит из одного атома) внутренняя энергия определяется соотношением

(14.1)

где — количество вещества газа (число молей), — универсальная газовая постоянная, — абсолютная температура. Заметим, что с помощью закона Клапейрона-Менделеева формула (14.1) может быть преобразована к виду

(14.2)

где — давление, — объем газа.

Внутренняя энергия тела может измениться при теплообмене, когда молекулы тела сталкиваются с более быстрыми или более медленными молекулами других тел и получают от них или отдают им энергию, или в процессе совершения механической работы над этим телом внешними силами. В связи с эти вводят следующие определения. Количеством теплоты, переданным некоторому телу, называют энергию, переданную этому телу в процессе хаотических столкновений молекул. Процесс передачи энергии в виде теплоты называют процессом теплопередачи. Если внешние силы не совершают над телом работы, для процесса теплопередачи справедливо следующее балансовое соотношение

(14.3)

где — изменение внутренней энергии тела, — количество переданной этому телу теплоты. Поскольку изменение внутренней энергии тела может быть и положительным , и отрицательным , из закона (14.3) следует, что количеству теплоты следует придать алгебраический смысл: если энергия передается телу, количество переданной этому телу теплоты нужно считать положительным , если забирается — отрицательным .

Внутренняя энергия тела изменяется при сжатии тела, трении и ряде других механических процессах. В этом случае на изменение внутренней энергии расходуется работа , совершаемая над телом внешними силами

(14.4)

(конечно, здесь подразумевается, что работа не расходуется на энергию движения тела как целого, а только на изменение внутреннего движения, т.е. все перемещения тела как целого или его макроскопических частей должны происходить бесконечно медленно). Очевидно, работа внешних сил положительна, если эти силы сжимают тело и его объем уменьшается, и отрицательна — если объем тела увеличивается. В первом случае, как это следует из (14.4), внутренняя энергия тела возрастает (), во втором убывает ().

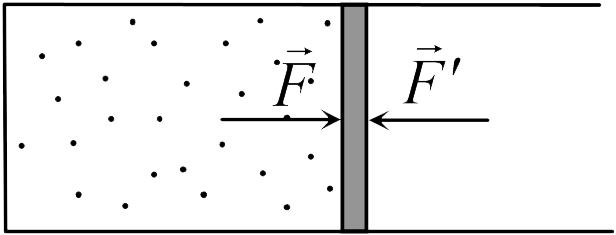
Одновременно с внешними силами при сжатии или расширении тел совершают работу и сами эти тела. Рассмотрим, например, газ, находящийся в цилиндрическом сосуде и отделенный от атмосферы поршнем (см. рисунок). И при сжатии, и при расширении газа силы, действующие на поршень со стороны газа, совершают над ним работу (в первом случае отрицательную, во втором положительную). При этом, поскольку поршень перемещается бесконечно медленно, силы, действующие на него со стороны газа и внешние силы практически равны друг другу как при сжатии, так и при расширении газа (в противном случае в балансе энергии необходимо было учитывать кинетическую энергию, приобретенную поршнем). Поэтому работа, совершенная газом и внешними силами над газом равны по величине, но отличаютсязнаком¹. Очевидно, работа газа положительна, если газ расширяется, и отрицательна, если газ сжимается.

При решении задач на термодинамику следует помнить одно важное свойство работы газа, которое во многих случаях позволяет ее легко вычислить. Работа газа в некотором процессе численно равна площади фигуры под графиком зависимости давления от объема в этом процессе. В частности в изобарическом процессе при давлении , в котором объем газа изменился от значения до значения , газ совершает работу (см. рисунок; площадь графика, соответствующая работе, выделена):

(14.5)

где — количество вещества газа, — изменение температуры в рассматриваемом процессе.

Если газ участвует в процессе, в котором одновременно имеет место и теплообмен, и совершается работа, то справедливо соотношение

(14.6)

которое называется первым законом термодинамики (здесь — работа газа).

Закон (14.6) позволяет найти одну из входящих в него величин, если заданы две других. Если задается только одна из величин, входящих в закон (14.6), но как-то определяется процесс, происходящий с газом, то две остальные величины могут быть определены. Например, в изохорическом процессе не совершается работа, поэтому

(14.7)

В изотермическом процессе не меняется внутренняя энергия газа, поэтому

(14.8)

В адиабатическом процессе (процессе без теплообмена с окружающей средой) , поэтому

(14.9)

В изобарическом процессе есть связь между изменением внутренней энергии газа и его работой. Из формул (14.1) и (14.5) заключаем, что работа одноатомного идеального газа и изменение его внутренней энергии в изобарическом процессе связаны соотношением

(14.10)

Для характеристики процессов нагрева-остывания тела вводят понятие теплоемкости тела , которая определяется как

(14.11)

где — количество теплоты, сообщенное телу в некотором процессе, — изменение его температуры в этом процессе. Подчеркнем, что и в формуле (14.11) не независимы, а связаны друг с другом: — это то изменение температуры, которое происходит благодаря сообщению телу количества теплоты . Поэтому теплоемкость (14.11) не зависит от и , а зависит от свойств тела и происходящего с ним процесса.

Если тело однородно, то его теплоемкость пропорциональна его массе . Поэтому отношение является характеристикой вещества тела и называется его удельной теплоемкостью. Удельная теплоемкость представляет собой экспериментально измеряемую (табличную) характеристику веществ. Из определения удельной теплоемкости следует, что если телу массой , изготовленному из вещества с удельной теплоемкостью , сообщить количество теплоты , то будет справедливо соотношение

(14.12)

где — изменение температуры тела.

Приведем теперь решения данных в первой части задач.

В задаче 14.1.1 внутренняя энергии газа увеличится согласно формуле (14.1) — ответ 1.

Для ответа на вопрос задачи 14.1.2 удобно использовать формулу для внутренней энергии газа в виде (14.2). По этой формуле находим, что внутренняя энергия увеличилась в 3/2 раза (ответ 2). Обратим внимание читателя, что причина изменения давления и объема может быть любой — ответ от этого не зависит. Может измениться или температура газа, или количество вещества, или и то и другое одновременно.

Поскольку температура и количество вещества газа не изменялись в рассматриваемом в задаче 14.1.3 процессе, внутренняя энергия газа не изменилась (ответ 3).

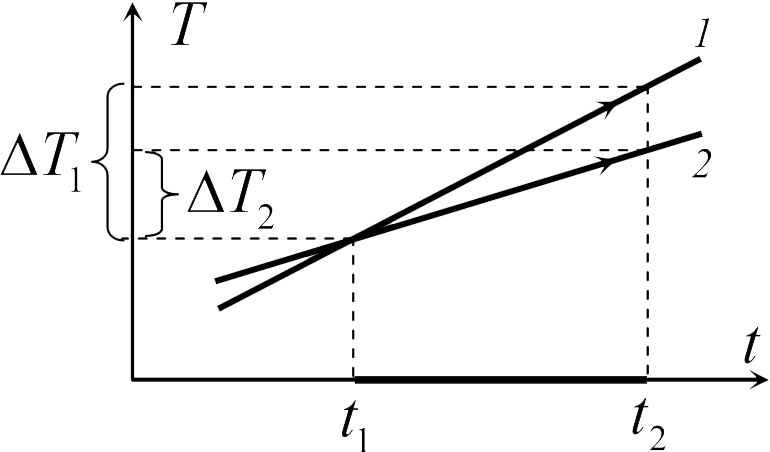
В задаче 14.1.4 следует воспользоваться определением теплоемкости (14.11). Для этого рассмотрим, например, ин-тервал времени , выделенный жирным на оси времени (см. рисунок). За этот интервал оба тела получили одинаковое количество теплоты , поскольку нагреватели одинаковы. Изменение температур тел и можно определить по графику — эти величины отмечены фигурными скобками на оси температур. Поскольку из формулы (14.11) заключаем, что — ответ 2.

В задаче 14.1.5 следует воспользоваться определением удельной теплоемкости. По формуле (14.12) находим

(ответ 1).

Для совершения работы необходимо механическое движение. Поскольку объем газа в задаче 14.1.6 не меняется, механическое движение отсутствует, работа газа равна нулю (ответ 4).

Применяя к рассматриваемому в задаче 14.1.7 процессу первый закон термодинамики (14.6) и учитывая, что в изохорическом процессе работа газа равна нулю, заключаем, что (ответ 3).

В изотермическом процессе не меняется внутренняя энергия идеального газа. Поэтому , и работа , совершенная над газом, определяется соотношением (14.4), (14.6): (задача 14.1.8 — ответ 2).

Адиабатический процесс происходит без теплообмена с окружающими телами: . Поэтому из первого закона термодинамики (14.6) получаем в задаче 14.1.9 для работы газа (ответ 2).

Применяя первый закон термодинамики (14.6) к процессу, происходящему с газом в задаче 14.1.10, найдем, что внутренняя энергия газа увеличилась на 10 Дж (ответ 2).

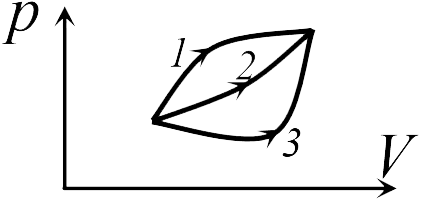
Для решения задачи 14.2.1 можно использовать то обстоятельство, что работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объема и осью объемов. Из рисунка следует, что наибольшей является площадь под графиком процесса 1. Поэтому бóльшую работу газ совершает в процессе 1 (ответ 1).

В задаче 14.2.2 следует применить ко всем трем процессам, графики которых даны на рисунке к решению предыдущей задачи, первый закон термодинамики (14.6) . Учитывая, что начальная и конечная температура газа во всех трех процессах одинакова, и, следовательно, одинаковы изменения внутренней энергии газа , а работа наибольшая в процессе 1 (см. решение предыдущей задачи), заключаем, что газ получил большее количество теплоты в процессе 1 (ответ 1).

Работа газа положительна, если газ расширяется. Для доказательства этого утверждения представим газ в сосуде, ограниченном подвижным поршнем. Если газ расширяется, то и перемещение поршня и сила, действующая на него со стороны газа, направлены одинаково, поэтому работа газа положительна. При сжатии газа его работа отрицательна. Поэтому в задаче 14.2.3 работа газа положительна в процессе 3 (ответ 3).

Так как графики процессов 1–2 и 3–4 в задаче 14.2.4 — прямые, проходящие через начало координат, эти процессы — изохорические, и газ не совершает в них работу. А поскольку изменение внутренней энергии газа в этих процессах одинаково, то одинаковы и количества теплоты, сообщенные газу в этих процессах (ответ 3).

Задача 14.2.5 аналогична предыдущей. Рассматриваемый процесс — изохорический, поэтому изменение внутренней энергии газа равно сообщенному количеству теплоты = 100 кДж (ответ 2).

Вычисляя площадь под графиком процесса в задаче 14.2.6, находим работу газа (ответ 2).

В условии задачи 14.2.7 дано количество теплоты , которое забрали у газа. Первый закон термодинамики, в который входит эта величина, имеет вид

где — работа, совершенная над газом в рассматриваемом процессе. Подставляя в эту формулу данные в условии величины, находим = –5 Дж (ответ 1).

Чтобы понять, расширялся или сжимался газ в рассматриваемом в задаче 14.2.8 процессе, из первого закона термодинамики найдем работу газа: если она окажется положительной, газ расширялся, если отрицательной — сжимался. Из закона (14.6) находим

Поэтому газ сжимался (ответ 1).

Чтобы найти долю количества теплоты, которая пошла на увеличение внутренне энергии газа в изобарическом процессе (задача 14.2.9) воспользуемся формулой (14.5) для работы газа в этом процессе . Поскольку изменение внутренней энергии одноатомного идеального газа равно , заключаем, что изменение внутренней энергии газа составляет 3/2 от его работы. Поэтому 2/5 количества теплоты, сообщенного газу в изобарическом процессе тратится на работу, 3/5 — на изменение внутренней энергии газа (ответ 3).

Чтобы найти теплоемкость газа в изотермическом процессе (задача 14.2.10), применим к этому процессу определение теплоемкости (14.11)

Поскольку в изотермическом процессе при ненулевом количестве сообщенной теплоты, то теплоемкость газа равна бесконечности. Это означает следующее — в изотермическом процессе газу сообщают теплоту, а он не нагревается, что и означает бесконечную теплоемкость газа (теплота расходуется только на совершение работы).