Глава 19. Проводники и диэлектрики в электрическом поле
В школьном курсе физики есть раздел, посвященный электрическим свойствам проводников и диэлектриков и их поведению во внешнем электрическом поле. В необходимый минимум знаний по этому вопросу входит понимание явления электростатической индукции и его механизмов в проводниках и диэлектриках, а также умение находить в простейших ситуациях индуцированные в проводниках и диэлектриках заряды. Кратко рассмотрим эти вопросы.
В состав атомов входят заряженные частицы (электроны и протоны). Поэтому любое тело содержит огромное количество зарядов. Число протонов и число электронов в составе незаряженного тела одинаково, заряженное тело содержит разные количества протонов и электронов.
В зависимости от того, являются ли заряды внутри тела свободными или связанными, все вещества делятся на проводники, диэлектрики (или изоляторы) и полупроводники. В проводниках электрические заряды могут свободно перемещаться, и потому такие тела проводят электрический ток. К проводникам относятся все металлы, в которых носителями заряда являются «оторвавшиеся» от атомов валентные электроны (свободные электроны), а также растворы электролитов (кислот, щелочей и солей), в которых перемещаются положительные и отрицательные ионы.
В диэлектриках все заряды «привязаны» к покоящимся атомам и не могут перемещаться. Поэтому диэлектрики не проводят электрический ток. К диэлектрикам, например, относятся: газы, пластмассы, эбонит, резина, дистиллированная вода.
Вещества, занимающие по своей проводимости промежуточное положение между проводниками и диэлектриками, называются полупроводниками. Типичными полупроводниками являются кристаллические германий и кремний. В полупроводниках свободные носители заряда есть, но их мало. Не следует, однако, думать, что полупроводники являются просто «плохими» проводниками или «плохими» изоляторами. Промежуточная проводимость полупроводников приводит ко многим необычным их свойствам, которые отличают полупроводники как от проводников, так и от диэлектриков. С этими свойствами связаны многие применения полупроводников в технике.
При помещении проводника в электрическое поле свободные носители заряда внутри проводника перемещаются и на его поверхности образуются области положительного и отрицательного заряда. Такое явление разделения зарядов в проводнике под действием внешнего электрического поля называется электростатической индукцией или поляризацией проводника. В результате поляризации электрическое поле в пространстве изменяется и становится равным сумме внешнего поля и поля индуцированных зарядов. Можно доказать, что перемещение зарядов в проводнике будет происходить до тех пор, пока суммарное поле внутри проводника не станет равным нулю, а на его поверхности — перпендикулярным поверхности.
Такое свойство проводника позволяет находить индуцированные на его поверхности заряды. Для этого нужно ввести эти заряды как некоторые неизвестные величины, затем найти поле, создаваемое этими зарядами и суммарное поле, равное векторной сумме внешнего поля и поля индуцированных зарядов, приравнять суммарное поле внутри проводника к нулю. Решение полученного уравнения и позволит найти индуцированные заряды.
В диэлектрике поляризация также происходит, однако механизмы этого явления — другие. Как правило, молекулы диэлектрика являются полярными, т.е. какая-то область молекулы заряжена положительно, какая-то — отрицательно. При помещении диэлектрика во внешнее поле молекулы поворачиваются, и на определенные участки поверхности диэлектрика «выходят» своими положительными областями, на другие — отрицательными. В результате на поверхности диэлектрика образуются области положительного и отрицательного заряда, но при разрезании диэлектрика (в отличие от разрезания проводника) получившиеся части будут незаряженными. Благодаря поляризации диэлектрика поле в нем ослабляется, но не становится равным нулю. Характеристика диэлектрика 
, которая показывает, во сколько раз ослабляется поле в нем, называется диэлектрической проницаемостью.
Рассмотрим в рамках данного фактического материала задачи первой части.
В задаче 19.1.1 из нижеперечисленного списка веществ проводником электрического тока является металл — свинец (ответ 3).
В задаче 19.1.2 диэлектриком является мел (ответ 1; алюминий и железо — металлы, т.е. проводники тока, в водопроводной воде растворены различные соли в таком количестве, что она является прекрасным проводником электрического тока).
Как отмечалось ранее, при внесении металлического тела в электрической поле (задача 19.1.3) на поверхности тела индуцируются электрические заряды, сумма которых равна нулю. Все остальные предложенные ответы неверны: для приобретения электрического заряда телу нужно сообщить или забрать у него электроны, заряды не могут индуцироваться в объеме проводника — их невозможно там удержать.
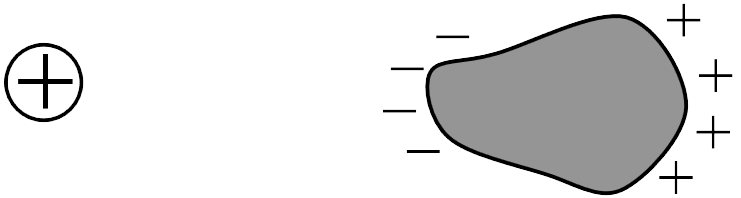
Взаимодействие между зарядом и незаряженным диэлектрическим телом возникает (задача 19.1.4), причем это взаимодействие –— притяжение (ответ 2). Это взаимодействие возникает благодаря поляризации: из-за ориентации молекул диэлектрика часть поверхности тела, обращенная к заряду, приобретает заряд противоположного знака, дальняя от заряда часть поверхности тела — заряд того же знака (см. рисунок).
|
Поэтому возникнет две силы — притяжение близких участков и отталкивание дальних. Но поскольку индуцированные заряды — одинаковы по величине, а кулоновское взаимодействие убывает с ростом расстояния, притяжение сильнее отталкивания, и тело будет притягиваться к заряду.
будет заряжена положительно, часть 
— отрицательно (ответ 2). Если тело является диэлектриком, то его части будут незаряженными (задача 19.1.6 — ответ 1).
и мысленно перенесем его из одной точки тела в другую (см. рисунок; траектория движения заряда показана пунктиром). С одной стороны, при таком движении поле совершит работу 
, где 
и 
— потенциалы начальной и конечной точек траектории тела. С другой стороны, поскольку напряженность поля внутри проводящего тела равна нулю, эта работа — нулевая. Поэтому 
(правильный ответ в задаче — 4). Аналогично в задаче 19.1.8 
(ответ ,3).После соединения проводником (задача 19.1.9) два металлических тела и соединяющий проводник будут представлять собой единое проводящее тело. Поэтому потенциалы любых точек этого тела должны быть одинаковы. Следовательно, выровняются потенциалы сфер (ответ 1).
В задачах с заземлением (задача 19.1.10) рассматривается следующая модель Земли: это проводящий шар с размерами, много большими размеров любых тел, имеющихся в задаче. Поэтому для потенциала Земли можно использовать формулу (18.8), которая для любых зарядов, с которыми мы имеем дело, дает нулевой результат. Поэтому при заземлении тела его потенциал становится равным нулю (ответ 2).
Сила взаимодействия противоположных электрических зарядов при внесении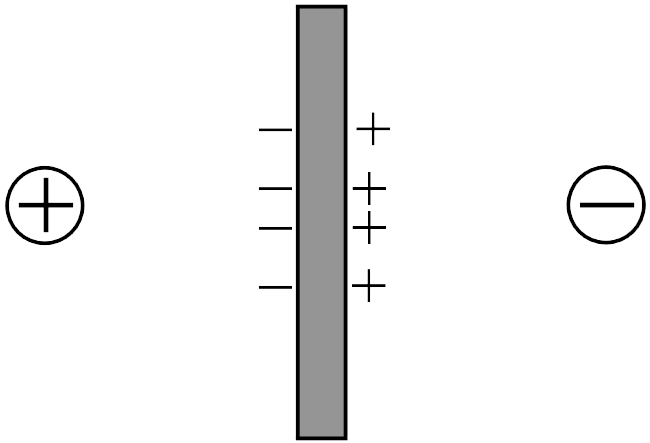 
между ними диэлектрической пластинки (задача 19.2.1) увеличится (ответ 2). Действительно, в поле зарядов на поверхности пластинки будут индуцироваться заряды: ближе к положительному — минусы, ближе к отрицательному — плюсы (см. рисунок). В результате на каждый точечный наряду с той же самой силой притяжения к другому заряду (а она, конечно, не меняется, ведь принцип суперпозиции говорит о том, что все заряды взаимодействуют независимо) будут действовать две дополнительные силы. Это будет сила притяжения к зарядам того же знака и отталкивания от зарядов противоположного. А поскольку заряды противоположного знака ближе, сила притяжения будет больше. Возникновение дополнительной силы, направленной к пластинке, будет восприниматься как увеличение силы притяжения.
Как отмечалось выше (задача 19.1.7) потенциал электрического поля во всех точках проводящего тела одинаков. Поэтому можно ввести понятие потенциала проводящего тела, который определяется как потенциал электрического поля в любой точке этого тела. Поэтому для потенциала металлического шара из задачи 19.2.2 имеем 
, где 
, 
— заряд шара, 
— его радиус. Потенциал поля шара на расстоянии двух радиусов от его поверхности и, следовательно, трех радиусов от центра шара равен 
, т.е. одной трети от потенциала шара. Отсюда находим 
В (ответ 2).
Потенциал каждой капли ртути (задача 19.2.3) равен 
, где 
, 
— заряд капли, 
— ее радиус. После слияния заряд большой капли равен 
, а радиус 
, где 
— число капель (последнее следует из того, что объем большой капли равен сумме объемов капель). Отсюда находим потенциал большой капли
|
(ответ 2).
Поскольку после соединения шары будут представлять собой единое металлическое тело (задача 19.2.4), то заряд разделится между ними так, что потенциалы шаров будут одинаковы. Поэтому для зарядов шаров 
и 
выполнено условие
|
Отсюда находим 
(ответ 4).
Согласно принципу суперпозиции потенциал каждой точки складывается из потенциала, создаваемого в этой точке всеми зарядами. Поэтому потенциалы и внутренней и внешней сферы (задача 19.2.5) создаются зарядами внутренней и внешней сфер. А поскольку потенциал в любой точке внутри сферы определяется ее радиусом сферы (см. (18.8)), получаем
|
Аналогично находим потенциал внешней сферы
|
Отсюда находим
|
(ответ 3).
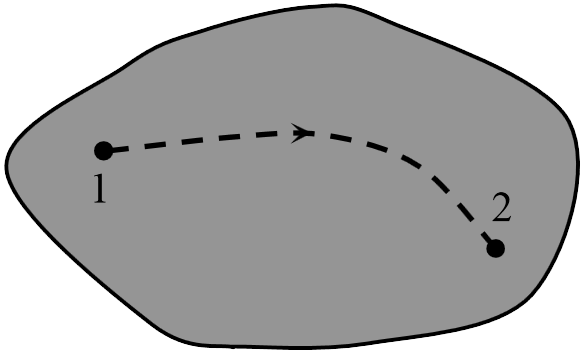
Чтобы найти разность потенциалов между двумя проводниками нужно мысленно перенести пробный заряд с одного из них на другой, найти работу, совершаемую электрическим полем при этом, разделить работу на величину пробного заряда. В задаче 19.2.6 между пластинками будет однородное поле с напряженностью 
. Поэтому работа поля над пробным зарядом 
при его перемещении с одной пластинки на другую есть 
. С другой стороны, работа поля следующим образом связана с разностью потенциалов 
. Отсюда находим разность потенциалов пластин
|
(ответ 3).
Поскольку напряженность поля между двумя параллельными пластинками, заряженными одинаковым зарядом равна нулю (см. задачу 18.2.8), то при перенесении пробного заряда с одной пластины на другую поле не совершает работу. Следовательно, разность потенциалов между такими пластинками в задаче 19.2.7 равна нулю (ответ 4).
В задаче 19.2.8 заряды распределятся только по внешней поверхности полого шара (если бы весь заряд или какая-то его часть находилась на внутренней поверхности, то в объеме проводника было бы электрическое поле, чего быть не должно). А поскольку заряд, расположенный на поверхности сферы, создает поле только снаружи этой сферы, то напряженность будет отлична от нуля только в области 3. Поэтому правильный ответ в задаче — 4.
В задаче 19.2.9 заряды индуцируются и на внешней и на внутренней поверхностях полого шара, причем их сумма равна нулю. Результирующее поле будет создаваться центральным зарядом и индуцированными зарядами, которые, фактически, представляют собой равномерно заряженные сферы. А поскольку поле сферы равно нулю внутри этой сферы, то суммарное поле в полости (в области 1) равно полю точечного заряда, т.е. не равно нулю. Внутри металлического тела (в области 2) поле равно нулю, как и внутри любого проводника. Снаружи шара поля индуцированных зарядов компенсируют друг друга, поэтому суммарное поле равно полю точечного заряда, т.е. не равно нулю. Поэтому правильный ответ в этой задаче — 2.
В задаче 19.2.10 на внешней и внутренней поверхности сферической оболочки будут индуцироваться такие заряды, что суммарное поле (внешнее плюс поле индуцированных зарядов) внутри оболочки будет равняться нулю. Пусть на внутренней поверхности будет индуцирован заряд — 
, тогда на внешней поверхности будет индуцирован заряд 
. Поле внутри оболочки (в области 2) будет создаваться только точечным зарядом и зарядами внутренней поверхности (заряд внешней поверхности благодаря ее сферичности в этой области электрического поля не создает). С другой стороны это поле равно нулю. Отсюда заключаем, что заряд внутренней поверхности оболочки противоположен по знаку центральному точечному заряду и равен ему по величине 
. Следовательно, заряд внешней поверхности оболочки центральному заряду (ответ 1).