Глава 21. Электрический ток. Законы Ома и Джоуля-Ленца

Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.

Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени

(21.1)

Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю. Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.

Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то

(21.2)

Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21.2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид

(21.3)

Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова resistance — сопротивление).

Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения

(21.4)

где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.

Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников

(21.4)

Если участок цепи представляет собой несколько однородных проводников 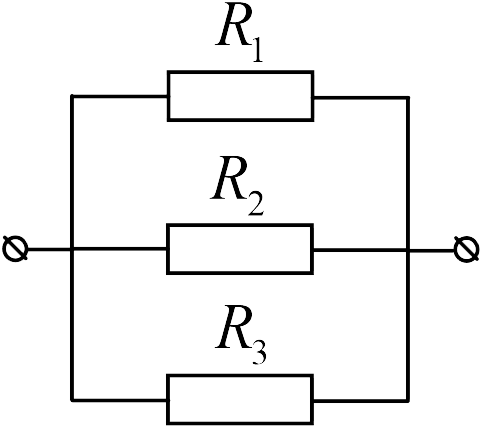с сопротивлениями , соединенных параллельно (см. рисунок), то электрическое напряжение на каждом проводнике будет одинаковым , ток через участок будет равен сумме токов, текущих через каждый проводник , а величина, обратная эквивалентному сопротивлению всего участка, равно сумме обратных сопротивлений отдельных проводников

(21.5)

Рассмотрим теперь закон Ома для замкнутой электрической цепи.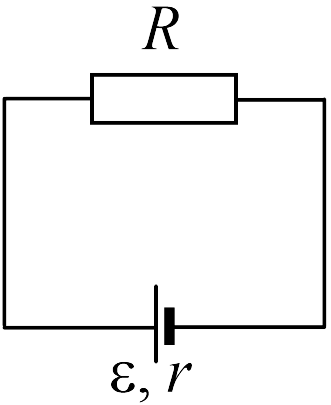 Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду

(21.6)

В этом случае сила тока в цепи равна

(21.7)

Формула (21.7) называется законом Ома для замкнутой электрической цепи.

При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно

(21.8)

(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения. Поэтому отношение

(21.9)

которое называется мощностью тока, не зависит от времени наблюдения. Формулу (21.9) также называют законом Джоуля-Ленца.

Рассмотрим теперь задачи.

Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21.1.1 — ответ 2).

Согласно определению (21.1) находим среднюю силу тока в канале молнии (задача 21.1.2)

(ответ 2).

Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).

По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21.1.4)

Таким образом, сила тока уменьшилась в 4 раза (ответ 3).

Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем. Поэтому в задаче 21.1.5 имеем, например, используя крайнюю точку графика

(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.

Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6

где — удельное сопротивление меди, — длина проводника, — его радиус. Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем

(ответ 3).

Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21.1.7) сила тока в проводнике не изменится (ответ 4).

В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21.7). Имеем

где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).

В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому

где — внутреннее сопротивление источника (ответ 3).

Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (задача 21.1.10) приведет к увеличению мощности тока в 4 раза (ответ 2).

В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).

Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21.2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.

Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.

Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно

(ответ 2).

Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что

(ответ 2).

При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что

(ответ 1).

Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка

а затем и эквивалентное сопротивление всей цепи

(ответ 3).

При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т.к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).

Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна

где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:

(ответ 2).

Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —

(ответ 1).

Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22.8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца

где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).