Глава 4. Сила трения

Сила трения возникает при скольжении шероховатых тел по шероховатым поверхностям, или при попытке сдвинуть такие тела вдоль поверхностей. Чтобы сформулировать основные законы, которым подчиняется сила трения, рассмотрим несколько случаев.

Тело аккуратно положили на горизонтальную поверхность, а затем подействовали на него горизонтальной силой , которую в дальнейшем мы будем называть сдвигающей. Очевидно, что если сдвигающая сила не достаточна, чтобы сдвинуть тело, то сила трения равна силе (в частности, при нулевой внешней силе сила трения равна нулю — шероховатости тела и опоры «не зацепляются»).

Поскольку тело, свободно лежащее на какой-то поверхности, можно сдвинуть, прикладывая к нему достаточно большую сдвигающую силу, то сила трения между телом и этой поверхностью не может превышать некоторого максимального значения, которое, как это следует из опыта, определяется соотношением

(4.1)

где — некоторое число, называемое коэффициентом трения, — сила нормальной реакции, действующая между телом и поверхностью. Если тело скользит по поверхности, то, как это также следует из опыта, на тело действует сила трения, равная своему максимальному значению (4.1).

Из этого краткого обзора свойств силы трения следуют правила анализа этой силы. Если в условии задачи говорится, что тело движется по некоторой поверхности, то для силы трения следует использовать закон (4.1) с силой реакции, которую можно найти из проекции второго закона Ньютона на ось, перпендикулярную этой поверхности. Далее с помощью второго закона Ньютона можно исследовать движение тела. Если же задача поставлена так, что тело кладут на поверхность и действуют на него какими-нибудь силами, причем неизвестно, сдвигают эти силы тело, или нет, то требуется дополнительный анализ силы трения. Необходимо сравнить сдвигающую силу (которой является проекция суммарной силы на ось, параллельную поверхности) и максимальную силу трения (4.1). Если сдвигающая сила меньше максимальной силы трения, тело будет покоиться, а сила трения равняться сдвигающей силе. Если сдвигающая сила больше максимальной силы трения (4.1), тело будет двигаться, а действующая на него сила трения будет определяться формулой (4.1). Разберем эти и другие свойства силы трения на примере решения задач.

Очевидно, коэффициент трения — безразмерная величина. Действительно, в формуле (4.1) и , и имеют размерность силы, поэтому коэффициент трения — безразмерный (задача 4.1.1 — ответ 4).

В задаче 4.1.2 тело не движется, и никакие силы не стремятся его сдвинуть. Поэтому шероховатости тела и опоры «не зацепляются» и сила трения равна нулю (ответ 2).

В задаче 4.1.3 тело движется по шероховатой горизонтальной поверхности, поэтому сила трения определяется формулой (4.1) и равна (ответ 1).

Из условия задачи 4.1.4 не ясно, будет двигаться данное тело, или нет. Сравнение сдвигающей силы и максимальной силы трения показывает, что данной сдвигающей силы не достаточно, чтобы сдвинуть тело. Следовательно, тело будет покоиться, а сила трения равняться сдвигающей силе (ответ 2). Из этого анализа следует также, что сдвинуть данное тело может минимальная горизонтальная сила (задача 4.1.5 — ответ 3).

Аналогичный анализ необходимо выполнить, когда исследуется поведение тела на наклонной плоскости (задача 4.1.6). Если тело аккуратно положить на плоскость, то в зависимости от коэффициента трения и угла наклона плоскости оно может как покоиться, так и скользить. Очевидно, для тела на наклонной плоскости сдвигающей силой является составляющая силы тяжести, параллельная плоскости, т.е.

(см. рисунок). Сила реакции плоскости компенсирует составляющую силы тяжести, перпендикулярную плоскости, и потому равна (параллельная и перпендикулярная плоскости составляющие силы тяжести показаны на рисунке пунктирными стрелками). Поэтому телу будет двигаться, если

(4.2)

или (ответ 2). Или (задача 4.1.7 — ответ 1). Ускорение тела, соскальзывающего с наклонной плоскости, можно найти из второго закона Ньютона (задача 4.1.8)

Для наклонной плоскости высотой 3 и длиной 5 м , . Отсюда находим, что (ответ 2).

В задачах 4.1.9 и 4.1.10 необходимо выразить коэффициент трения между телом и поверхностью через кинематические характеристики движения тела по этой поверхности. Основная идея решения заключается в том, чтобы из кинематических характеристик найти ускорение тела, а затем из второго закона Ньютона — силу и коэффициент трения. Из законов равноускоренного движения (2.2) и (2.3) находим связь времени движения до остановки и пройденного расстояния

Отсюда получаем . С другой стороны из второго закона Ньютона для тела, движущегося по шероховатой горизон — тальной поверхности, следует, что . Поэтому (задача 4.1.9 — ответ 3).

Аналогично в задаче 4.1.10 из закона равноускоренного движения для скорости ( — начальная скорость, — время движения до остановки) и второго закона Ньютона получаем (ответ 1).

В нескольких следующих задачах 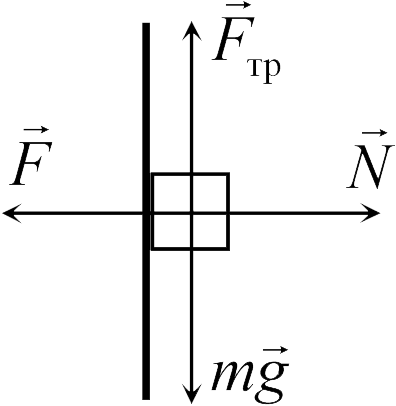также необходимо исследовать возможность движения тела под действием тех или иных сдвигающих сил. В задаче 4.2.1 сдвигающей силой является сила тяжести, а сила реакции и сила трения возникают благодаря прижиманию тела к стенке внешней силой (см. рисунок). Поэтому . Отсюда заключаем, что брусок будет покоиться, пока сила тяжести будет меньше максимальной силы трения . Или (ответ 3).

В задаче 4.2.2 сдвигающей силой является горизонтальная составляющая внешней силы , т.е. . Сила реакции поверхности, как это следует из проекции второго закона Ньютона на вертикальное направление, равна . Поэтому тело начнет двигаться, если . Или

(ответ 1).

Согласно второму закону Ньютона при действии на тело двух взаимно перпендикулярных горизонтальных сил и , сдвигающая сила равна . Поскольку по условию задачи 4.2.3 при и тело движется с пренебрежимо малым ускорением, то . Откуда получаем (ответ 4).

В задаче 4.2.4 цепочка начинает соскальзывать со стола, когда сила тяжести, действующая на свисающий со стола конец цепочки ( ) , сравнивается с максимальной силой трения, действующей на ее часть, лежащую на столе ( ) . Поэтому (ответ 2).

График зависимости силы трения от сдвигающей силы (задача 4.2.5) строится следующим образом. При малых значениях сдвигающей силы тело покоится, а сила трения равна сдвигающей силе. Когда же сдвигающая сила превосходит максимальную силу трения , то сила трения не зависит от сдвигающей силы:

График, правильно представляющий эту зависимость, дан на рисунке 4.

Аналогичные рассуждения позволяют построить график зависимости ускорения тела от сдвигающей силы (задача 4.2.6). Для значений сдвигающей силы, не превосходящих максимальную силу трения, тело покоится и его ускорение равно нулю. Если сдвигающая сила превосходит максимальную силу трения , ускорение тела находится из второго закона Ньютона: . Правильный график приведен на рисунке 1.

На тело со стороны наклонной плоскости в задаче 4.2.7 действуют перпендикулярная плоскости сила реакции и сила трения, направленная вверх вдоль плоскости, причем поскольку тело движется, сила трения достигает своего максимального значения. Чтобы найти направление вектора суммы этих сил заметим, что поскольку первоначально тело покоилось на плоскости, то в этом положении сумма силы нормальной реакции и силы трения, которая меньше максимальной, направлена вертикально вверх. Поэтому правильный ответ для направления суммы сил трения и реакции в случае движения тела вниз по плоскости дает рисунок 2.

Движение тела в задаче 4.2.8 в системе отсчета, связанной с лентой, происходит следующим образом. На покоящуюся ленту попадает тело, имеющее скорость , замедляется под действием силы трения, а затем останавливается. При этом пока тело перемещается относительно ленты, на него действует постоянная сила трения . Поэтому ускорение тела постоянно и равно . Применяя закон равноускоренного движения для скорости (2.3) к моменту остановки тела относительно ленты

где — время, прошедшее от начала движения тела по ленте до его остановки, получаем (ответ 2).

Очевидно, правильным графиком зависимости скорости от времени в задаче 4.2.9 является график 1. Действительно, после остановки в верхней точке тело начнет соскальзывать по плоскости вниз, так как (задача 4.1.6). Следовательно, график 3. не подходит. При движении тела вниз проекция его скорости на ось отрицательна, поэтому не подходит и график 4. А поскольку ускорение тела при его движении вверх больше ускорения при движении вниз , наклон второй части графика зависимости скорости от времени должен быть меньше его наклона при движении вниз.

При движении тела по доске в задаче 4.2.10 на доску в горизонтальном направлении действуют силы трения со стороны тела и со стороны поверхности , направленные так, как показано на рисунке. Это значит, что сила трения, действующая на доску со стороны тела, стремится заставить ее двигаться, со стороны поверхности — не дать доске двигаться. Поэтому поведение доски определяется сравнением этих сил. А поскольку сила трения между доской и телом равна ( — масса тела, сила трения выражена в Ньютонах), максимальная сила трения между доской и поверхностью — ( — масса доски, сила трения также выражена в Ньютонах), то доска будет двигаться (ответ 1).