Глава 8. Закон всемирного тяготения

Массивные тела, даже находящиеся на больших расстояниях друг от друга, притягиваются друг к другу. Такое взаимодейст-вие называется гравитационным. Закон гравитационного взаимодействия тел был установлен Ньютоном на основе анализа имеющихся в его распоряжении экспериментальных данных и называется законом всемирного тяготения. Закон всемирного тяготения утверждает, что два точечных тела с массами и , находящиеся на расстоянии друг от друга, притягиваются друг к другу с силой

(8.1)

где — коэффициент пропорциональности, который называется гравитационной постоянной.

Обратим внимание 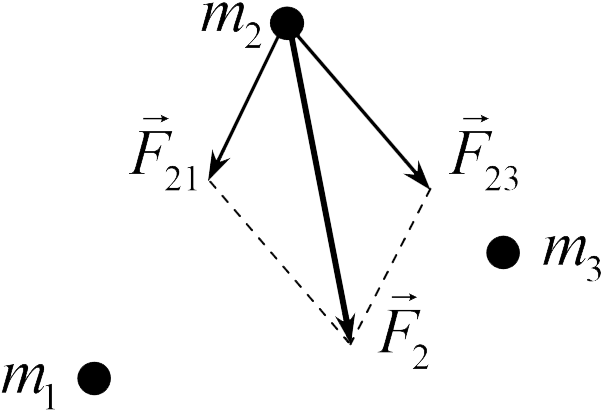читателя на то, что закон всемирного тяготения в форме (8.1) справедлив только для точечных тел. Для нахождения силы гравитационного взаимодействия протяженных тел используется принцип суперпозиции гравитационных сил. В соответствии с этим принципом силы гравитационного взаимодействия в системе из трех точечных тел можно вычислить, находя силы взаимодействия каждой пары тел друг к другу по формуле (8.1) и складывая затем векторы этих сил. Например, чтобы найти силу , действующую на массу в системе тел , и (см. рисунок), нужно найти силу , действующую на тело со стороны тела (при этом можно использовать закон всемирного тяготения в форме (8.1)). Затем по закону всемирного тяготения нужно найти силу , действующую на тело со стороны тела , а затем сложить получившиеся векторы

(8.2)

(аналогичным образом можно найти силу, действующую на другие массы и ). Принцип суперпозиции дает рецепт поиска гравитационных сил, действующих между протяженными (неточечными) телами. Такие тела нужно мысленно разделить на точечные части, найти силу взаимодействия каждой пары точечных частей, просуммировать полученные вектора (число которых, вообще говоря, бесконечно большое). В математике разработаны методы такого суммирования, но в программу школьного курса физики эти методы не входят. Нужно знать только, что такая процедура существует и уметь применять ее в простейших случаях, когда суммирование выполняется элементарно на основе свойств симметрии тел. Кроме того, нужно знать, что для тел сферической формы, находящихся вне друг друга, применение принципа суперпозиции приводит в точности к закону всемирного тяготения в форме (8.1), в котором — расстояние между центрами тел (это утверждение впервые доказал Ньютон, разработав для выполнения бесконечного суммирования основы математического анализа). Из последнего утверждения следует, что для силы тяжести точечного тела массой , находящегося на поверхности некоторой планеты сферической формы, справедливо соотношение

(8.3)

где и — масса и радиус планеты. С другой стороны, сила тяжести описывается соотношением . Поэтому из формулы (8.3) получаем выражение для ускорения свободного падения на поверхности планеты через ее массу и радиус

(8.4)

В задачах на закон всемирного тяготения часто рассматривают вращательное движение спутников вокруг планет. Если спутник движется с выключенным двигателем, то существует определенное соотношение между его скоростью и радиусом орбиты. Действительно, при движении со скоростью по окружности радиуса спутник имеет ускорение , которое сообщается ему гравитационной силой (другие силы на спутник не действуют). Поэтому второй закон Ньютона для спутника дает

(8.5)

Откуда находим

(8.5)

Если рассматриваются орбиты, расположенные на небольшой высоте над поверхностью планеты, когда в формуле (8.6) практически совпадает с радиусом планеты, скорость (8.6) называется первой космической скоростью для данной планеты. Рассмотрим применение этих соотношений и законов к решению задач.

В задаче 8.1.1 рассматриваются точечные тела, поэтому для вычисления силы их взаимодействия используем закон все-мирного тяготения (8.1). Из него следует, что при увеличении в 3 раза расстояния между этими телами сила их гравитационного притяжения уменьшается в 9 раз (ответ 4).

Если массу одного точечного тела увеличить в 2 раза, а массу второго увеличить в 3 раза при неизменном расстоянии между телами (задача 8.1.2), то из закона (8.1) следует, что сила их гравитационного взаимодействия увеличится в 6 раз (ответ 3). Аналогично из закона (8.1) находим, что в задаче 8.1.3 сила взаимодействия тел уменьшится 8 раз (ответ 3).

Применяя формулу (8.4) для ускорения свободного падения на поверхности планеты и на таком расстоянии от центра, когда ускорение свободного падения равно половине его значения на поверхности, получаем (задача 8.1.4)

Из этих формул заключаем, что (ответ 1).

Из формулы (8.4) следует, что отношение ускорений свободного падения на поверхности двух планет с массами и радиусами , и , равно

Поэтому в задаче 8.1.5 получаем для ускорения свободного падения на поверхности Марса

(ответ 2).

В задаче 8.1.6 используется то обстоятельство, что гравитационное взаимодействие тел подчиняется третьему закону Ньютона: сила всемирного тяготения (8.1) действует как на одно, так и на другое тело. Поэтому из второго закона Ньютона заключаем, что ускорения этих тел относятся обратно отношению масс

(ответ 3).

Используя закон всемирного тяготения, получим для силы притяжения Меркурия и Земли к Солнцу (задача 8.1.7)

где — масса Солнца, и — массы Меркурия и Земли, и — расстояния от Меркурия и Земли до Солнца. Отсюда находим

(ответ — 2).

Из закона всемирного тяготения для ракеты (задача 8.1.8) следует, что сила притяжения ракеты к Земле уменьшается в 4 раза по сравнению с силой притяжения на поверхности, если расстояние от ракеты до центра Земли возрастает вдвое. Это значит, что ракета будет находиться на расстоянии, равном радиусу Земли от поверхности (ответ 1).

В задаче 8.1.9 будем использовать принцип суперпозиции. Силы, действующие на центральное тело со стороны двух других тел, показаны на рисунке. По закону всемирного тяготения находим силу, действующую на центральное тело со стороны левого тела

и силу, действующую на центральное тело со стороны правого тела

Поскольку эти силы направлены противоположно, находим, что результирующая сила равна

(ответ 3).

Очевидно, силы, действующие на тело, находящееся в вершине прямого угла (задача 8.1.10) направлены под прямым углом друг к другу (см. рисунок) и определяются законом всемирного тяготения . Поэтому результирующая сила направлена по биссектрисе прямого угла и равна

(ответ 2).

Ускорение свободного падения тела массой определяется соотношением

(1)

где — гравитационная сила, действующая на тело. Очевидно, что не зависит от массы тела, поскольку гравитационная сила пропорциональна массе этого тела, которая, таким образом, сокращается в отношении (1) (задача 8.2.1 – ответ 4).

Как говорилось во введении к настоящей главе, сила притяжения сферических тел определяется законом всемирного тяготения в форме (8.1), в котором — расстояние между их центрами. Поэтому в задаче 8.2.2 сила притяжения двух шаров определяется формулой (2).

Сила взаимодействия двух одинаковых шаров с массой и радиусом , касающихся друг друга, равна (задача 8.2.3)

Для ответа на вопрос задачи эту силу удобно выразить через плотность и радиус. Используя определение плотности ( , где — объем шаров), получаем

Из этой формулы следует, что сила взаимодействия двух касающихся шаров при их фиксированной плотности пропорциональна четвертой степени их радиуса. Поэтому при увеличении радиуса вдвое сила взаимодействия возрастет в 16 раз (ответ 4).

Согласно принципу суперпозиции для нахождения силы, действующей на точечное тело, помещенное в центр массивного кольца, со стороны этого кольца (задача 8.2.4), необходимо мысленно разбить кольцо на точечные части, вычислить силы, действующие на тело со стороны этих частей и просуммировать найденные векторы. Очевидно, благодаря симметрии задачи мы получим нуль, поскольку для каждого малого участка кольца найдется противоположный (см. рисунок), который даст такую же по величине, но противоположно направленную силу (ответ 4).

Когда тело движется на малой высоте над поверхностью планеты, его ускорение равно , где — первая космическая скорость, — радиус планеты. С другой стороны ускорение тела равно ускорению свободного падения на поверхности . Поэтому ускорение свободного падения на поверхности планеты из задачи 8.2.5 равно

(ответ 1).

Первая космическая скорость определяется формулой (8.6). Поэтому правильный ответ в задаче 8.2.6 — 3. Чтобы ответить на вопрос об изменении первой космической скорости при изменении радиуса и массы планеты, но неизменной плотности (задача 8.2.7), удобно выразить скорость (8.6) через плотность и радиус планеты

Отсюда следует, что при фиксированной плотности планеты первая космическая пропорциональна ее радиусу (ответ 2).

Для Земли вычисления первой космической скорости по формуле из решения задачи 8.2.5 дают: , где — ускорение свободного падения на поверхности Земли, — радиус Земли. Поэтому правильный ответ в задаче 8.2.8 — 3.

Весом тела называется сила, с которой тело действует на опору и которая равна по величине силе реакции опоры. Сила реакции опоры может обратиться в нуль по двум причинам. Во-первых, если нет силы тяжести, которая бы действовала на тело и прижимала бы его к опоре. А во-вторых, если сила тяжести есть, но она сообщает и телу и опоре одинаковые ускорения, в результате чего тело к опоре не прижимается. Именно второй случай реализуется в космическом корабле, свободно вращающемся вокруг Земли (задача 8.2.9). Сила тяжести здесь, конечно, есть (в противном случае корабль не вращался бы, а двигался прямолинейно и равномерно). Но поскольку сила тяжести, действующая на любое тело, пропорциональна его массе, она сообщает и кораблю и всем телам внутри него одинаковые ускорения. В результате корабль и все тела внутри него постоянно «падают» на Землю с одинаковыми ускорениями и, следовательно, вес этих тел внутри корабля равен нулю (ответ 3).

При свободном круговом движении спутника вокруг планеты его скорость и радиус орбиты связаны друг с другом соотноше-нием (8.6). Эта связь возникает потому, что на данной орбите гравитационная сила сообщает определенное ускорение, которое совпадает с центростремительным ускорением только при определенной скорости спутника. А если скорость спутника уменьшить по сравнению с этой скоростью (задача 8.2.10)? Тогда для сохранения орбиты спутника потребуется меньшая центростремительная сила (так как уменьшится его центростремительное ускорение). А поскольку гравитационная сила на той же орбите не изменится необходимо направить силу тяги двигателя так, чтобы сумма гравитационной силы и силы тяги была направлена к центру орбиты, а по величине была меньше гравитационной силы. Это значит, что сила тяги должна быть направлена противоположно гравитационной силе (ответ 3).