Выпуклость функции

Дифференцируемая в интервале (a; b) функция f(x) выпукла тогда и только тогда её производная возрастает.

(1) Функция выпукла и x₁ < x₂

f(x) ≥ f(x₁) + f ′(x₁)(x − x₁), f(x) ≥ f(x₂) + f ′(x₂)(x − x₂)

f(x₂) ≥ f(x₁) + f ′(x₁)(x₂ − x₁), f(x₁) ≥ f(x₂) + f ′(x₂)(x₁ − x₂)

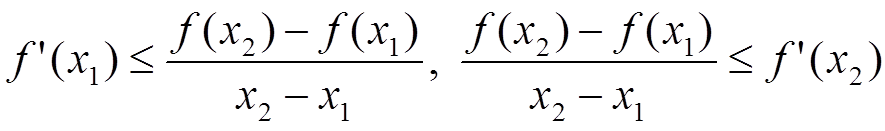
f ′(x₁) ≤ f ′(x₂).