Кривизна плоской кривой

φ(t) = a + R cos t, ψ(t) = b + R sin t

φ′(t) = −R sin t, ψ′(t) = R cos t

φ″(t) = −R cos t, ψ″(t) = R sin t

φ′(t)ψ″(t) − φ″(t)ψ′(t) = −(R sin t)(R sin t) − (R cos t)(R cos t) = −R²

|φ′(t)|² + |ψ′(t)|² = R² sin² t + R² cos² t = R²

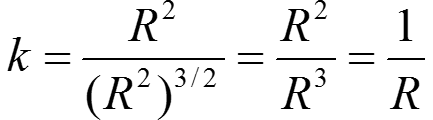
Часто представляется удобным приближенно заменять кривую вблизи рассматриваемой точки — окружностью, имеющую ту же кривизну, что и кривая в данной точке.

Кругом кривизны кривой в данной точке M называется круг, который

• касается кривой в точке M;
• направлен выпуклостью вблизи этой точки в ту же сторону, что и кривая;
• имеет ту же кривизну, что и кривая в точке M.

Центр круга кривизны называется центром кривизны, а радиус этого круга — радиусом кривизны (в данной точке). Для радиуса кривизны, очевидно, имеем формулу

(k — кривизна кривой)