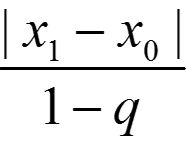Метод итераций (последовательных приближений)

Оценим, теперь, величину

|x_k − x₀| = |(x_k − x_k−1) + (x_k−1 − x_k−2) + … + (x₁ − x₀)| ≤

≤ q^k−1|x₁ − x₀| + q^k−2|x₁ − x₀| + … + |x₁ − x₀| =

= (q^k−1 + q^k−2 + … + 1)|x₁ − x₀| = 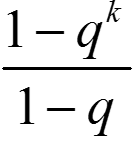|x₁ − x₀| ≤ .

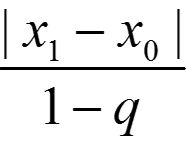Итак, мы имеем два неравенства

|x_m − x_n| ≤ qⁿ|x_m−n − x₀|, |x_k − x₀| ≤ ,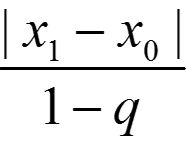

Из которых следует, что при m ≥ n

|x_m − x_n| ≤ qⁿ