Метод итераций (последовательных приближений)

∃ x = 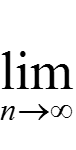x_n

(1) a ≤ x_n ≤ b ⇒ x ∈ [a, b]

(2) 0 ≤ |φ(x_n) − φ(x)| ≤ q|x_n − x| ⇒ φ(x_n) → φ(x)

(3) x_n = φ(x_n−1) ⇒ x = φ(x)

|x_m − x_n| ≤ qⁿ 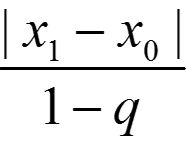, m → ∞ ⇒ |x − x_n| ≤ qⁿ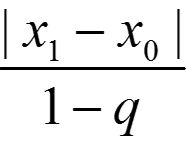

|x − x_n| = |x_n − x|, |x₁ − x₀| = |φ(x₀) − x₀|

⇓

|x_n − x| ≤ 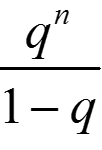|φ(x₀) − x₀|

Единственность решения

x = φ(x), y = φ(y)

|x − y| = |φ(x)− φ(y)| ≤ q|x − y|

(1 − q)|x − y| ≤ 0

|x − y| ≤ 0

x = y