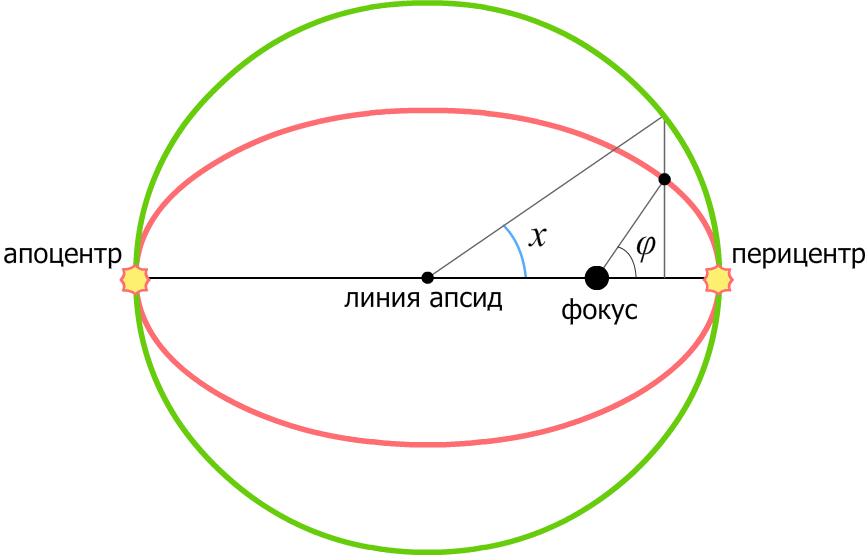
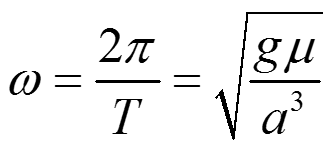Уравнение Кеплера

φ — истинная аномалия x — эксцентрическая аномалия T — период обращения μ = m1 + m2 (среднее движение) t — время движения от перицентра m = ωt — средняя аномалия

φ(x) = m + ε sin x

[a, b] = [m − 1, m + 1]

φ′(x) = ε cos x ⇒ |φ′(x)| ≤ ε

|φ(x) − φ(y)| = |φ′(ξ)(x − y)| ≤ ε(x − y)

Таким образом, итерации x_n = m + ε sin x_n–1 сходятся к единственному решению этого уравнения.