Экспоненциальная форма комплексного числа. Функции комплексного переменного

Если для e^z мы хотим сохранить правила действий со степенями, то w = e^z = e^a + bi = e^a · e^ib. Если z₁ = a₁ + ib₁, z₂ = a₂ + ib₂, то w₁ · w₂ = e^z₁ · e^z₂ = e^a₁ · e^a₂ · e^i(b₁+b₂) и сравнивая это с правилом умножения комплексных чисел в тригонометрической форме, следует считать, что |w| = e^a, |e^ib| = 1, а b — обобщённый аргумент числа w.

e^ib = cos b + i sin b

Тогда комплексное число w приобретает экспоненциальную форму записи

w = |w| · e^{i arg w}

Обозначение: e^iφ = cos φ + i sin φ.

Умножение любого z на e^iφ означает поворот вектора z на угол φ против часовой стрелки. Поэтому z = |z|e^iφ. В такой форме произведение чисел z₁ = |z₁|e^iφ₁ и z₂ = |z₂|e^iφ₂ имеет вид: z₁ · z₂ = |z₁||z₂|e^{i(φ₁+φ₂)}.

Связь с тригонометрией: e^−iφ = cos φ − i sin φ. Отсюда

и

Открывается возможность определения функции переменной z:

,

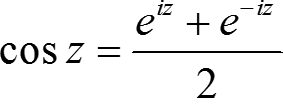e^z = e^x (cos y + i sin y) для z = x + iy