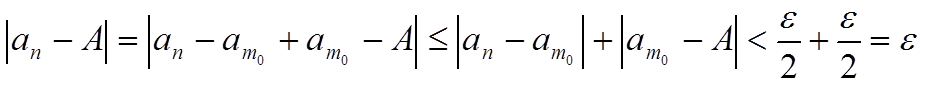Фундаментальные последовательности

Def.

Последовательность {a_n} называется фундаментальной, если

∀ ε > 0 ∃ N = N_ε: ∀ n, m > N → |a_n − a_m| < ε

Свойство 1

Фундаментальная последовательность ограничена.

Пусть m₀ > N. Тогда множество членов последовательности a_n с номерами n > N ограничено, поскольку
a_m0 − ε < a_n < a_m0 + ε.

Свойство 2

Предельная точка фундаментальной последовательности является пределом.

Пусть A — предельная точка: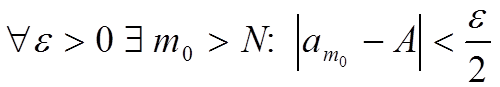

Последовательность фундаментальная: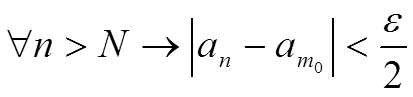

Объединение