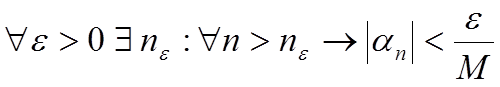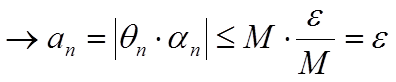Теорема о связи сходящейся и бесконечно малой последовательностями

Теорема 3

Пусть {a_n} — сходящаяся последовательность и Тогда a_n = A + α_n, где α_n — б.м.п.

Доказательство

Пусть α_n = a_n − A. Тогда ∀ ε > 0 ∃ n_ε: ∀ n > n_ε → |α_n| = |a_n − A| < ε.

Теорема 4

Сумма двух б.м.п. есть б.м.п., т. е. o(1) + o(1) = o(1).

Доказательство

Пусть α_n, β_n — б.м.п.

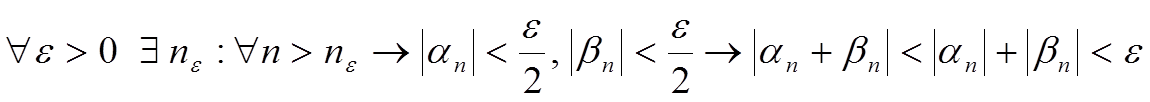
Теорема 5

Пусть α_n — б.м.п., θ_n — ограниченная последовательность. Тогда a_n = θ_n · α_n — б.м.п.

Доказательство

|θ_n| ≤ M, ∀ n,