Арифметические теоремы

Теорема 6

Пусть {a_n}, {b_n} — сходящиеся последовательности:

Тогда А)    Б)    C) 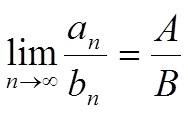, B ≠ 0

Доказательство

А) Т.3 ⇒ a_n = A + α_n, b_n = B + β_n, ⇒ a_n + b_n = A + B + α_n + β_n,

     Т.4 ⇒ α_n + β_n = o(1) Т.3 ⇒

Б) a_nb_n = (A + α_n)(B + β_n) = AB + α_nB + β_nA + α_nβ_n

     Т.4 ⇒ α_nB = o(1), β_nB = o(1), α_nβ_n = o(1),

C) 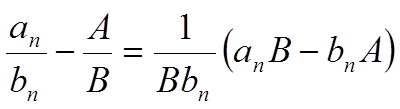 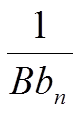   — ограниченная, (a_nB − b_nA) = o(1)