Теорема о переходе к пределу в неравенствах

Теорема 7

Пусть {a_n}, a ≥ 0 — сходящаяся последовательность:

  Тогда A ≥ 0

Доказательство

Предположим, что A < 0    

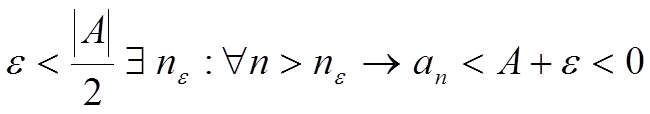
Следствие

Пусть {a_n}, {b_n} — сходящиеся последовательности:

  и a_n ≥ b_n ∀n.

Тогда A ≥ B

Доказательство

Для θ_n = a_n − b_n выполнены условия Т.7 ⇒ A ≥ B