Определение предела функции по Коши и Гейне и их эквивалентность

Теорема 1

Если число A — предел функции в точке a по Коши, то A — предел той же функции по Гейне и наоборот.

Доказательство

Пусть A — предел по Гейне — не является пределом по Коши.

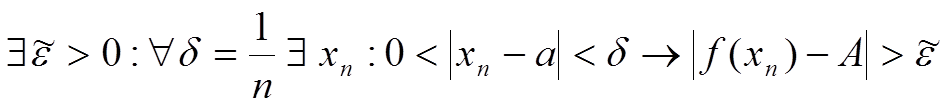
Для последовательности {x_n} и по Гейне

Пусть A — предел по Коши ∀ε > 0 ∃ δ_ε: ∀x: 0 < |x − a| < δ_ε → |f(x) − A| < ε

Для последовательности {x_n}

∃ n_δε: ∀n > n_δε → |x_n − a| < δ_ε → |f(x_n) − A| < ε