Непрерывность функции в точке. Арифметические теоремы о непрерывных функциях. Непрерывность сложной функции

Def.

Функция y = f(x) непрерывная в точке x = a, если

Def.

Функция y = f(x) непрерывная в точке x = a, если

Δf = f(a + Δx) − f(a) = o(1)

Пример 1

Доказать непрерывность функции y = x² в точке x = 1.

Δy = (1 + Δx)² − 1 = Δx·(2 + Δx) = o(1)

Пример 2

Доказать, что функция 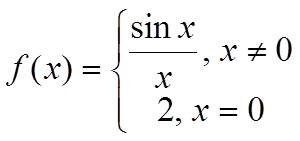разрывная в точке x = 0 и непрерывная в точках x ≠ 0.

Непрерывность функции по Гейне