Непрерывность функции в точке. Арифметические теоремы о непрерывных функциях. Непрерывность сложной функции

Теорема 1

Пусть функции y = f(x) и y = g(x) непрерывная в точке x = a. Тогда функции f(x) + g(x), f(x) · g(x) и 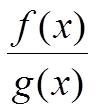(g(a) ≠ 0) непрерывные в точке x = a.

Def.

Функция y = f(g(x)) называется композицией функций y = f(z) и z = g(x).

Пример 3

Функция является композицией функций и z = x² + 1.