Непрерывность функции в точке. Арифметические теоремы о непрерывных функциях. Непрерывность сложной функции

Теорема 2

Функция z = g(x) непрерывная в точке x = a функция y = f(z) непрерывная в точке z = g(a).

Тогда композиция y = f(g(x)) непрерывная в точке x = a.

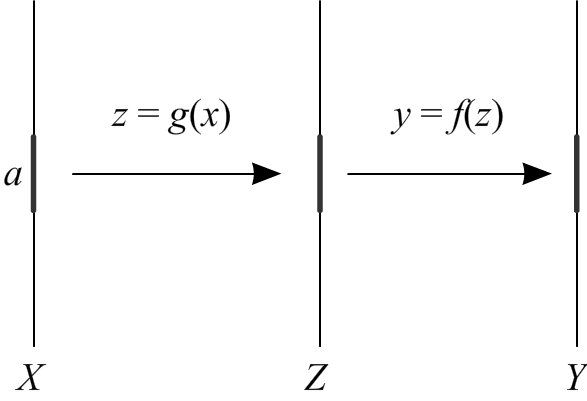
Доказательство

∀ ε > 0 ∃ δ₁ > 0: → |f(z) − f(g(a))| < ε, ∀ z ∈ U_δ1(g(a))

∃ δ₂ > 0: → |g(x) − g(a)| < δ₁: ∀ x ∈ U_δ2(a)

∀ x ∈ U_δ2(a) → z = g(x) ∈ U_δ1(g(a)) → |f(g(x)) − f(g(a))| < ε