Необходимое условие дифференцируемости

Теорема

Если функция дифференцируема, то она непрерывна.

Доказательство

Согласно доказанной выше теореме

f(x) − f(a) = f ′(a)(x − a) + α(x)(x − a).

Поэтому

f(x) = f(a) + f ′(a)(x − a) + α(x)(x − a).

Отсюда следует, что

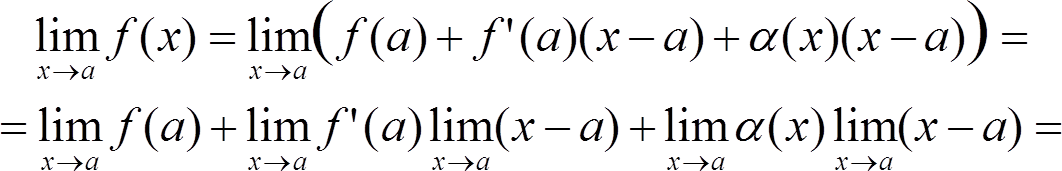
f(a) + f ′(a)·0 + 0·0 = f(a).

Так как предел функции равен значению в предельной точке, то функция непрерывна.