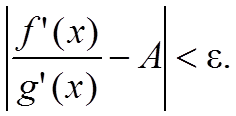Правило Лопиталя
Так как x ∈ (a; bε), то также и точка ξ ∈ (a; bε). В силу выбора интервала (a; bε)
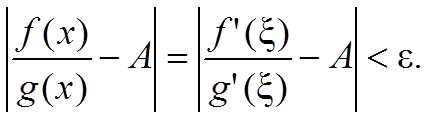
Поэтому A является пределом отношения функций при x → a + 0.
Пусть функции f(x) и g(x) определены и дифференцируемы в некотором интервале (a; b). Причём всюду в этом интервале производная g′(x) ≠ 0. Пусть также при x → b − 0 обе функции имеют пределы, равные нулю. Кроме того
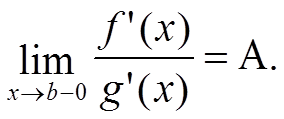
Тогда также и
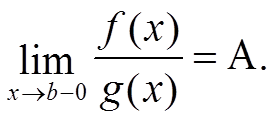
Так как обе функции имеют конечные пределы, то их можно доопределить по непрерывности на промежуток (a; b], полагая
f(b) = 0 и g(b) = 0.
Проверим определение предела для отношения функций и числа A. Возьмём положительное число ε. Из определения предела следует, что существует такой интервал (aε; b), в котором