Основные правила вычисления интегралов

Пример

$$\int{\frac{dx}{\sqrt{1 + x^2}}} = \begin{vmatrix} t = \ce{arctg} \, x \\ x = \ce{tg} \, t \\ dx = \frac{dt}{\cos^2{t}} \end{vmatrix} = \int{\frac{dt}{\cos^2{t} \sqrt{\ce{tg}^2 \, t +1}}} = \int{\frac{\cos{t} dt}{\cos^2{t}}} = $$ $$= \int{\frac{d \sin{t}}{1 - \sin^2{t}}} = \begin{vmatrix} t = \arcsin{z} \\ \sin{t} = z \\ \cos{t} dt = dz \end{vmatrix} = \int{\frac{dz}{1 - z^2}} = \frac{1}{2} \int{\left (\frac{1}{1 - z} + \frac{1}{1 + z}\right )} dz = $$ $$= \frac{1}{2} \left (-\int{\frac{d\left (1 - z \right )}{1 - z}} + \int{\frac{d\left (1 + z \right )}{1 + z}} \right ) = \frac{1}{2} \left (- \ln{ \left | 1 - z \right |} + \ln{ \left | 1 + z \right |} \right ) + C = $$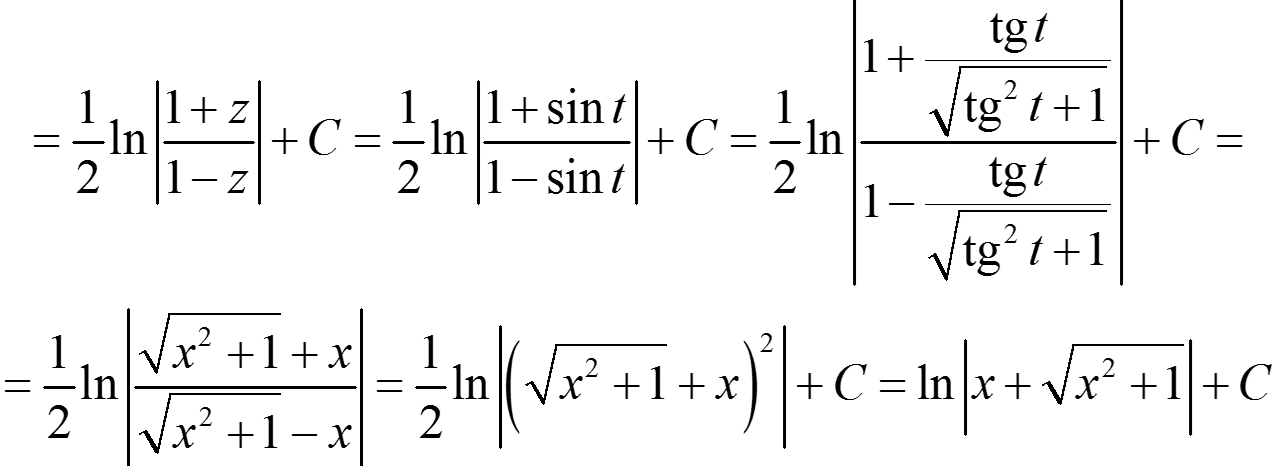

Получили табличный интеграл: 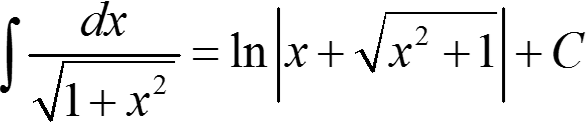.