Основные определения, примеры

Определение 1

Функция F(x) называется первообразной по отношению к функции f(x) на некотором промежутке, если на этом промежутке функция F(x) дифференцируема и удовлетворяет условию F′(x) = f(x) или, что то же самое, dF(x) = f(x)dx.

Пример 1

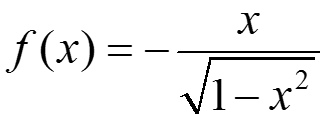— первообразная для на интервале (–1; +1), т. к. в любой точке этого интервала

.

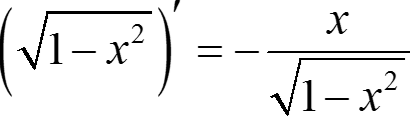Пример 2

F(x) = sin x — первообразная для f(x) = cos x на промежутке (–∞; +∞), т. к. ∀ x ∈ (–∞; +∞): (sin x)′ = cos x.

Пример 3

F(x) = arctg x — первообразная для на всей числовой прямой, т. к. .

Пример 4

— первообразная для 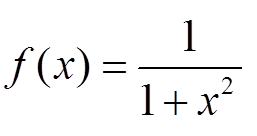на I = (−∞; 0) ∪ (0; +∞), т. к.

.
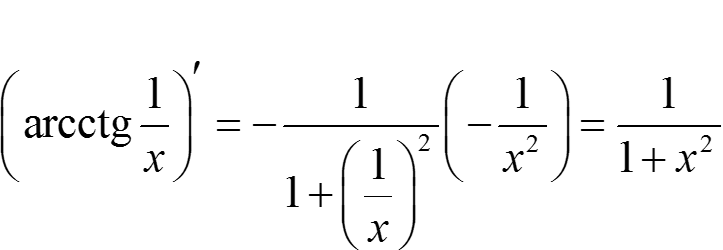