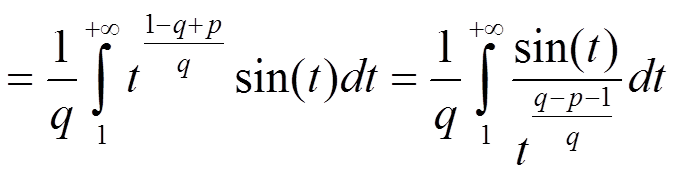Исследование функций на абсолютную и условную сходимость. Примеры

Пример № 2380

При каких значениях параметров p, q сходится интеграл

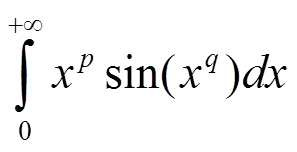
Решение № 2380

Пусть q > 0. Разобьём интеграл на сумму интегралов точкой x = 1.

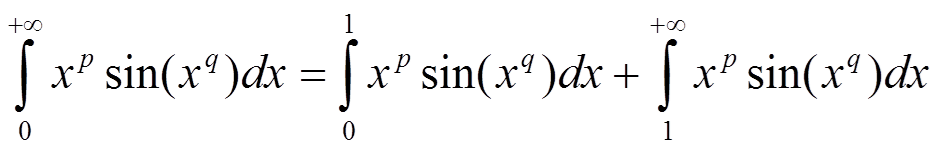
В окрестности x = 0 функция sin (x) эквивалентна x и вся подынтегральная функция эквивалентна степенной:

f(x) = x^p sin (x^q) ≈ x^p+q =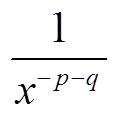

Тогда в окрестности x = 0 при q > 0 будет абсолютная сходимость при −p − q < 1, или p + q > −1, и интеграл будет расходиться при −p − q ≥ 1,   p + q ≤ −1.

Рассмотрим второй интеграл. Сделаем замену переменных с тем, чтобы воспользоваться признаком Дирихле–Абеля.