Решение № 2381

В области q < p несобственный интеграл первого рода расходится. Доказательство будем проводить по критерию Коши. Надо доказать, что

∃ ε > 0: ∀ b > 1 ∃ b₁ > b, ∃ b₂ > b: 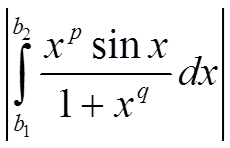> ε

Если степень 0 < q < p, то функция g(x)

g(x) = 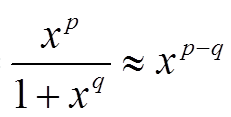при x → +∞

стремится к бесконечности при x, стремящемся к бесконечности.

Применим теорему о среднем для интегралов, тогда

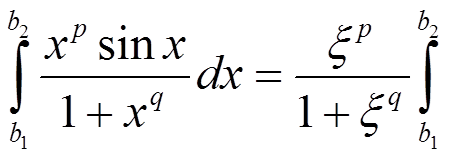sin xdx, где ξ ∈ [b₁, b₂]

∃ ε = 1 > 0: ∀ b > 1 ∃ k = [b] + 1 ∃ b₁ = 2πk > b, ∃ b₂ = 2πk + π > b:

В области q < p несобственный интеграл первого рода расходится по критерию Коши.

Рассмотрим плоскость переменных (p, q), и отразим на ней полученные неравенства.