Решение № 2381

Ответим на вопрос о сходимости интеграла первого рода от знакопеременной функции. Применим признак Дирихле–Абеля.

Функция sin x имеет ограниченную первообразную — (−cos x), функция g(x)

g(x) =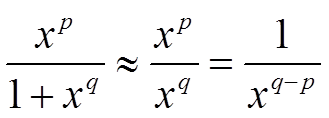

монотонно стремится к 0 при x, стремящемся к бесконечности при q − p > 0, тогда несобственный интеграл первого рода (на бесконечности) сходится при q > p.

Покажем, что в области

p < q ≤ 1 + p

интеграл из модулей расходится, тогда там будет условная сходимость.

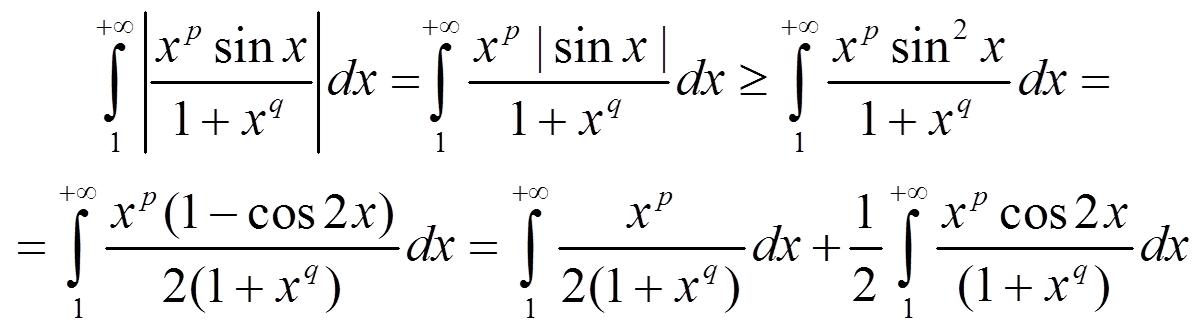
Второй из полученных интегралов сходится по признаку Дирихле–Абеля, а первый расходится по признаку сравнения со степенной функцией на бесконечности. Сумма сходящегося и расходящегося интеграла расходится. В области p < q ≤ 1 + p несобственный интеграл первого рода сходится условно.