Решение № 2381

2381

Исследовать на абсолютную и условную сходимость

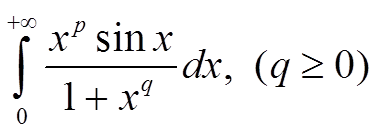
Решение № 2381

Разобьём интеграл на два, чтобы анализировать сходимость в окрестности 0 и окрестности бесконечности.

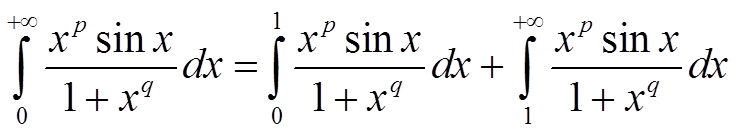
Рассмотрим первый интеграл. При x → 0 функция sin x эквивалентна x, подынтегральная функция эквивалентна

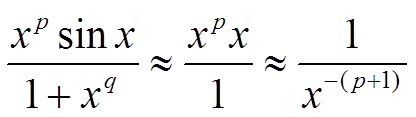
несобственный интеграл второго рода сходится абсолютно при любом q, и −(p + 1) < 1, или p > −2.

Рассмотрим второй интеграл в окрестности бесконечности.

При x, стремящемся к бесконечности, имеем знакопеременную функцию. Исследуем модуль

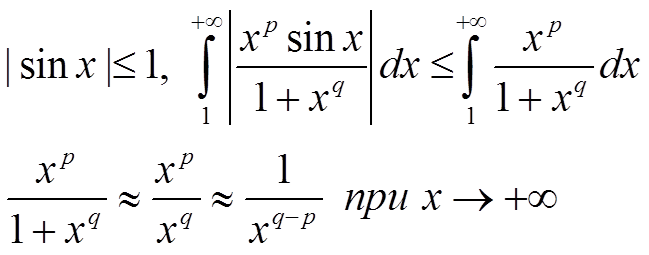
Несобственный интеграл первого рода сходится абсолютно при q − p > 1.