Вопросы

3. Если 1) сходится несобственный интеграл первого рода, и 2) существует конечный предел подынтегральной функции, то подынтегральная функция стремится к нулю.

Да, верно

Если существует конечный предел подынтегральной функции, то можно записать неравенство

= c ⇒ ∃ m: ∀ x > m верно, что

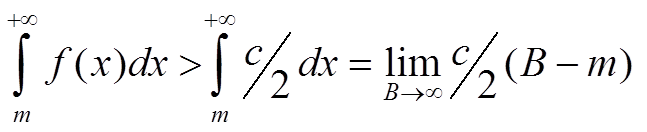
Конечный предел существует только при с = 0.

4. Если 1) сходится несобственный  интеграл первого рода, и 2) подынтегральная функция монотонна, то подынтегральная функция стремится к нулю.

Да, верно

Вопрос по несобственным интегралам второго рода

 Если подынтегральная функция стремится к бесконечности при x → b, то несобственный интеграл второго рода расходится.

Утверждение неверно

Это означает, что мы должны рассматривать несобственный интеграл второго рода.