Исследование сходимости интеграла. Примеры

2377

Исследовать сходимость интеграла

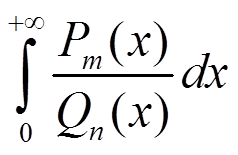
где P(x), Q(x) взаимно простые многочлены степени m, n соответственно.

Решение № 2377

Если знаменатель имеет действительные корни, то в окрестности каждого такого корня подынтегральная функция будет эквивалента

f(x) = 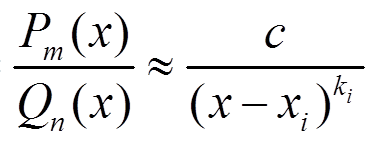при x → x_i

Так как степень больше либо равна 1, то интеграл будет расходиться. Первое условие сходимости — корни знаменателя не должны принадлежать области интегрирования.

В окрестности бесконечности подынтегральная функция будет эквивалентна

f(x) = 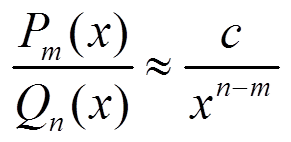при x → +∞

Несобственный интеграл первого рода будет сходиться при условии n − m > 1.

Ответ

Интеграл сходится, если корни знаменателя < 0, и n > m + 1.