Дифференцируемость функции

Следствие

Если точка x = a является внутренней точкой области определения функции f(x) и эта функция дифференцируема в точке

x = a, то дифференциал функции определяется равенством

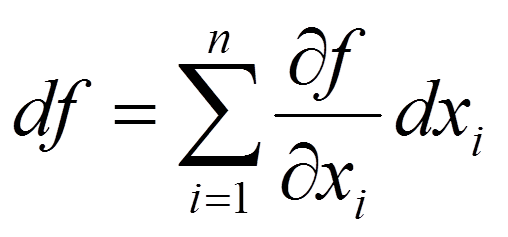
Достаточное условие дифференцируемости

Теорема

Пусть все частные производные функции f существуют в некоторой окрестности точки x = a и непрерывны в самой точке x = a, тогда функция f дифференцируема в точке x = a.

f(x₁, x₂, x₃, ..., x_n−1, x_n) − f(a₁, a₂, a₃, ..., a_n−1, a_n) =

= f(x₁, x₂, x₃, ..., x_n−1, x_n) − f(a₁, x₂, x₃, ..., x_n−1, x_n) +

+ f(a₁, x₂, x₃, ..., x_n−1, x_n) − f(a₁, a₂, x₃, ..., x_n−1, x_n) +

+ f(a₁, a₂, x₃, ..., x_n−1, x_n) − f(a₁, a₂, a₃, ..., x_n−1, x_n) +

+ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . +

+ f(a₁, a₂, a₃, ..., a_n−1, x_n) − f(a₁, a₂, a₃, ..., a_n−1, a_n).