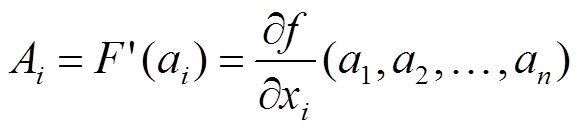Дифференцируемость функции

Доказательство (2)

Пусть

x = (a₁, ..., a_i−1, x_i, a_i+1, ..., a_n),

F(x_i) = f(x) = f(a₁, a₂, ..., a_i−1, x_i, a_i+1, ..., a_n).

В этом случае

|x − a| = |x_i − a_i|.

Так как a — внутренняя точка D(f), то существует шар |x − a| < R, целиком лежащий в D(f). Это означает, что при

|x_i − a_i| < R,

точка x попадает в D(f). т. е. a — внутренняя точка D(F).

При этом

F(x_i) − F(a_i) = A_i(x_i − a_i) + o(|x_i − a_i|).

Следовательно, функция F дифференцируема и