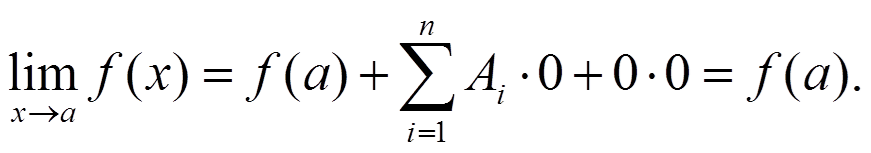Дифференцируемость функции

Необходимые условия дифференцируемости

Теорема

Пусть функция f(x) дифференцируема в точке x = a, тогда

1) Функция f(x) непрерывна в точке x = a.

2) Если a — внутренняя точка D(f), то в точке x = a существуют все частные производные, причём в представлении приращения функции

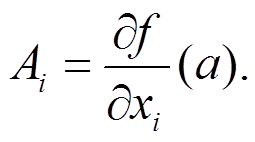
Доказательство (1)

Из представления приращения функции имеем

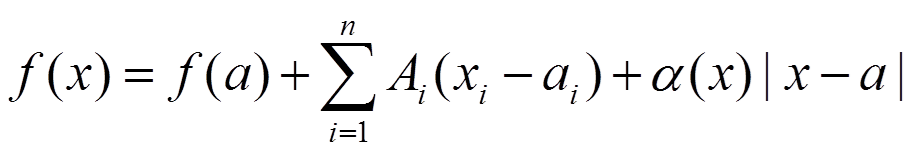
и в силу арифметических свойств предела